排序
排序是我们在计算的使用过程中,经常需要用到的操作。简单来说,就是将一个无序数据按照我们的要求进行重新排列,使其呈现出一定的顺序。
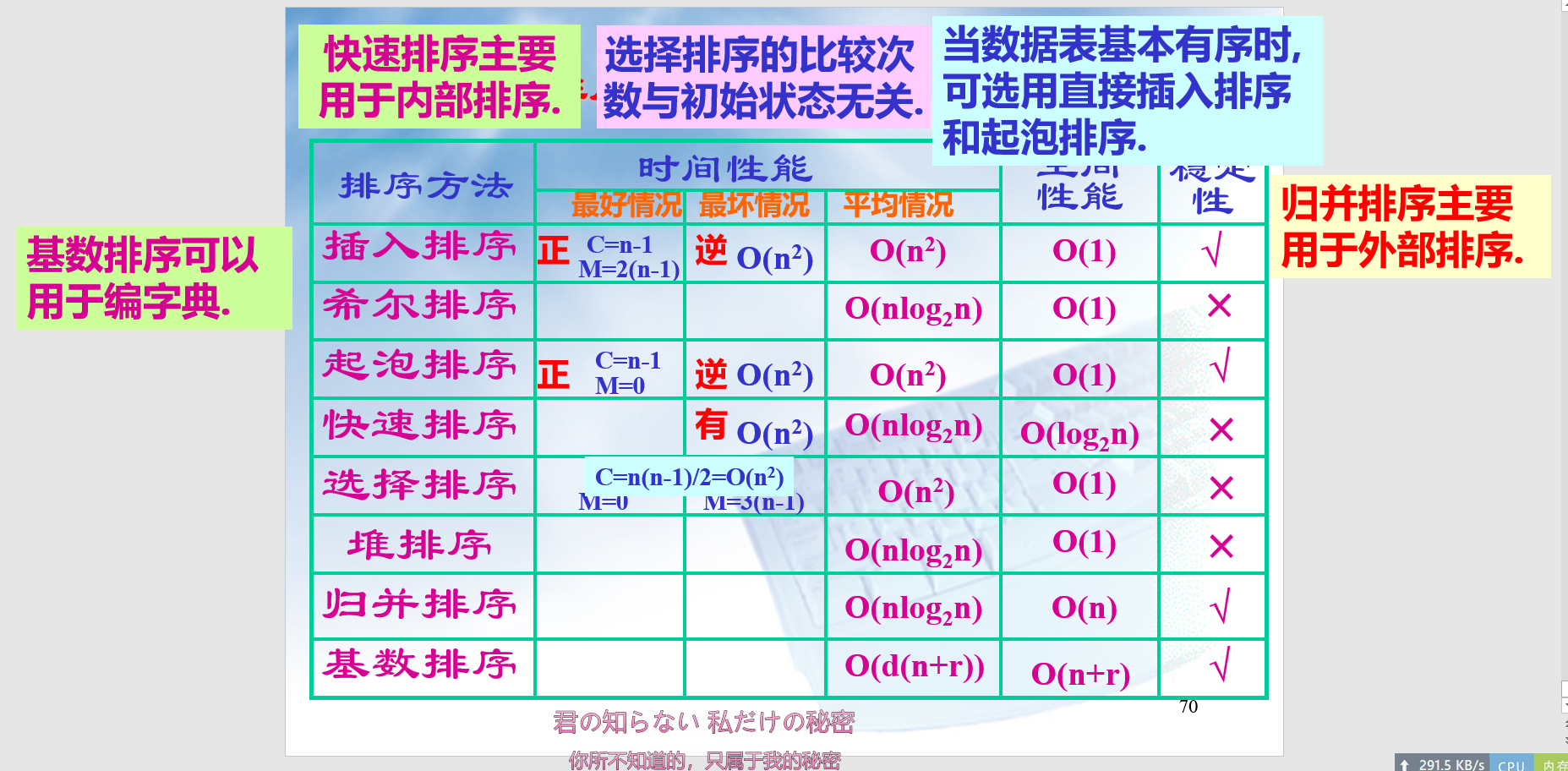
在谈到许多排序算法时,我们通常关心的是这个算法的时间复杂度和空间复杂度。
猴子排序
猴子排序,又称为 Bogo 排序,顾名思义,这个算法是将一个无序的数组进行胡乱排序(就像一个猴子一样),然后并查看其是否变得有序,因此最后数组是否变得有序了完全是一个概率性事件。这是一个效率十分十分低下的算法,在最坏的情况下其时间复杂度为 ∞,平均的时间复杂度也为 O(n * n !)。
伪代码如下:
function bogosort(arr)
while arr is not ordered
arr := 隨機排列(arr)
冒泡排序
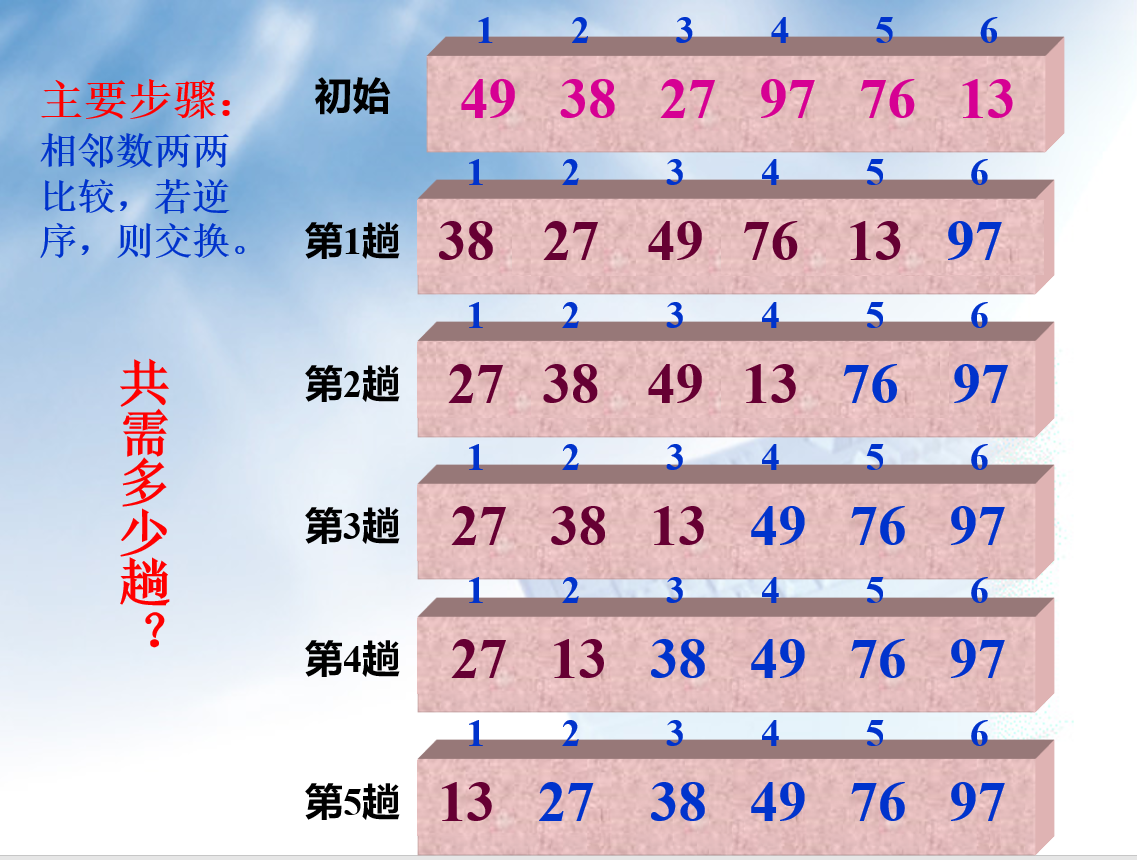
冒泡排序,又称为 bubble sort,由于其元素之间进行交换的方式犹如水中的气泡向上冒,故得名冒泡排序。
算法步骤如下:
- 比较相邻的元素,按照你的规则对元素进行交换(此处假设是让数组为非递减序列)
- 对每一对相邻得元素进行同样的操作,
- 针对所有的元素重复上述的步骤,除了已经排好序的元素
可以发现,对于冒泡排序,每进行一轮相当于是一个最大的数给冒泡至数组最末尾,然后第二轮是将第二大的数给冒泡至数组倒数第二的位置,依次循环。因此若共有 n 个数,只需进行 n - 1 躺即可。
从冒泡排序的特性可以看出来,当数组已经呈现有序的状态时,只需进行 n - 1 躺比较,而不需要对数组进行交换,而当数组完全逆序时,则是最坏的情况,在这时需要进行交换的次数最多。
平均时间复杂度为$O(n^2)$,空间复杂度为O(1)。另外,我们一般谈论的空间复杂度指的是完成这个算法需要开辟的额外空间,并不包括原本存储这些数据所花费的空间。
template<typename T> //整数或浮点数皆可使用,若要使用类(class)或结构体(struct)时必须重载大于(>)运算符
void bubble_sort(T arr[], int len) {
int i, j;
for (i = 0; i < len - 1; i++)
for (j = 0; j < len - 1 - i; j++)
if (arr[j] > arr[j + 1])
swap(arr[j], arr[j + 1]);
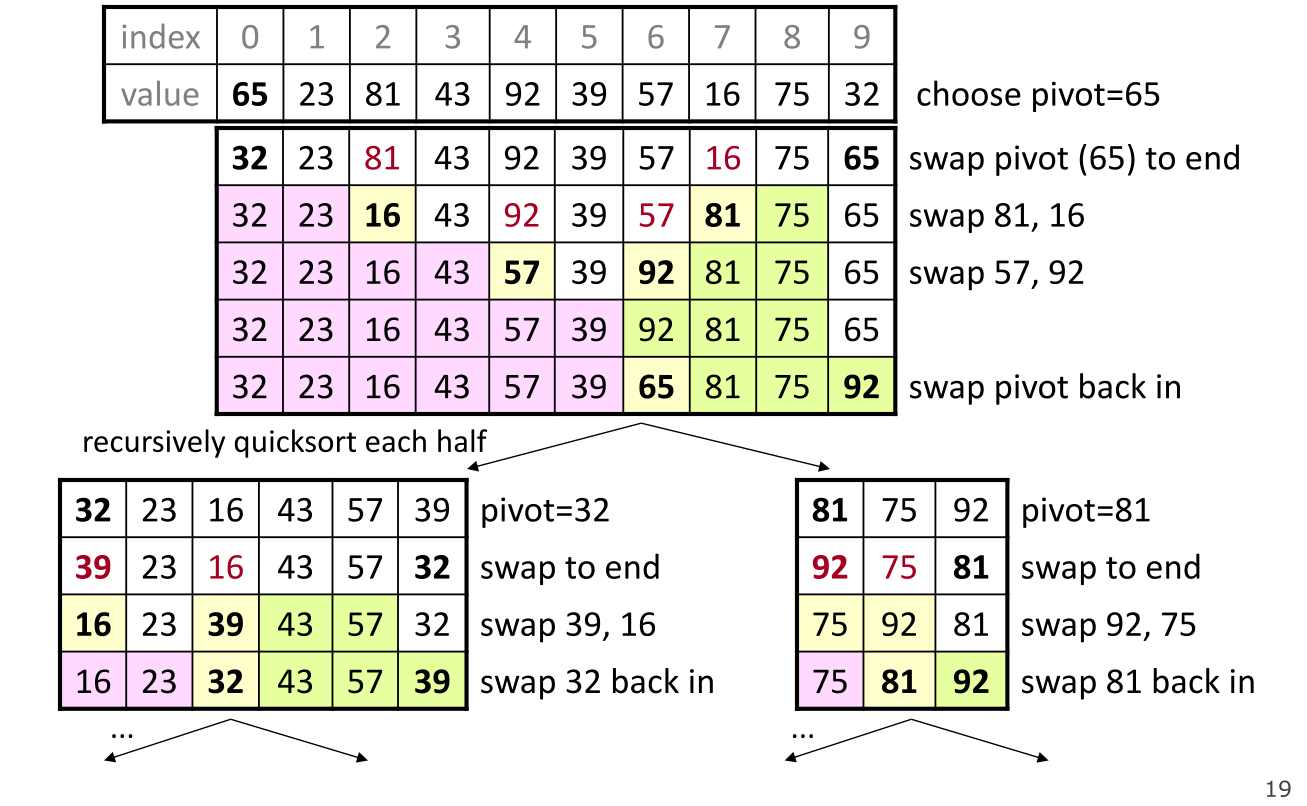
快速排序
快速排序主要采用了分治法,通过设置的某个基准,就数列划分为两组。
具体步骤如下:
- 从数列中挑选出一个元素,称为基准(pivot)(一般来说会选取最后一个元素作为基准值);
- 对数列重新排列,所有比基准值小的元素摆放在基准值的前面,所有比基准值大的元素摆放在基准的后面。在这个分区退出之后,基准就会位于数列的中间位置。该操作又被称为分区操作;
- 递归的把两个子序列再进行排序
或许这么说大家不能很理解,看一下下面这个图就知道了。
void quickSort(Vector<int>& v)
{
quickSortHelper(v, 0, v.size() - 1);
}
void quickSortHelper(Vector<int>& v, int min, int max)
{ if (min >= max)
{ // base case; no need to sort
return;
}
// choose pivot; we'll use the first element (might be bad!)
int pivot = v[min]; swap(v, min, max);// move pivot to end
// partition the two sides of the array
int middle = partition(v, min, max - 1, pivot);
swap(v, middle, max); // restore pivot to proper location
// recursively sort the left and right partitions
quickSortHelper(v, min, middle - 1);
quickSortHelper(v, middle + 1, max);
}
// Partitions a with elements < pivot on left and
// elements > pivot on right;
// returns index of element that should be swapped with pivot int
partition(Vector<int>& v, int i, int j, int pivot)
{
while (i <= j)
{
// move index markers i,j toward center
// until we find a pair of out-of-order elements
while (i <= j && v[i] < pivot) { i++; }
while (i <= j && v[j] > pivot) { j--; }
if (i <= j)
{
swap(v, i++, j--);
}
}
return i; }
// Moves the value at index i to index j, and vice versa.
void swap(Vector<int>& v, int i, int j)
{
int temp = v[i]; v[i] = v[j]; v[j] = temp;
}
对于快速排序算法,其平均的时间复杂度为 O(nlogn),空间复杂度为 O(logn)。
是一个稳定的排序。
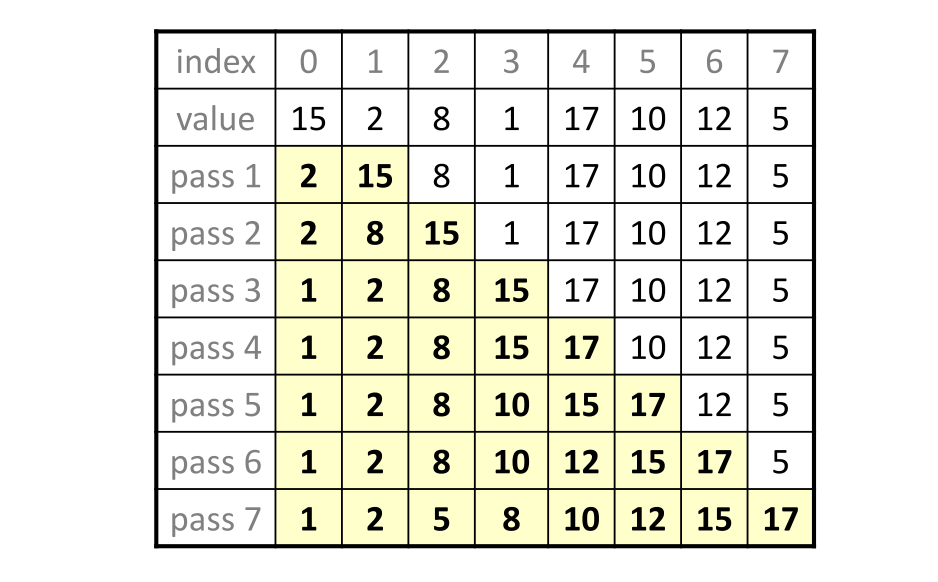
插入排序
当各位无法想起来插入排序的算法原理时,可以想一下我们打扑克牌洗手牌的操作,会把牌展开(看作数列),从左边第一张牌开始,然后是在第一张和第二张之间进行排序,如果第二张小于第一张,则将第二张牌插入到第一张牌的前面,再将情况扩展至3张牌,4张牌……..,直至对整个手牌完成排序。而插入排序所进行的算法也正是这这样的。具体步骤如下:
- 将第一待排序序列第一个元素看作一个有序序列,把第二个元素到最后一个元素当成是未排序序列;
- 从头到尾依次扫描为排序序列,将扫描到的每个元素插入到有序序列的适当位置,,使其仍然保持有序。
// Rearranges the elements of v into sorted order. void insertionSort(Vector<int>& v)
{
for (int i = 1; i < v.size(); i++)
{
int temp = v[i];
// slide elements right to make room for v[i]
int j = i;
while (j >= 1 && v[j - 1] > temp)
{ v[j] = v[j - 1];
j--;
}
v[j] = temp;
}
}
对于选择排序,其平均的时间复杂度为 $O(n^2)$, 空间复杂度为 O(1)。
是一个稳定的排序。
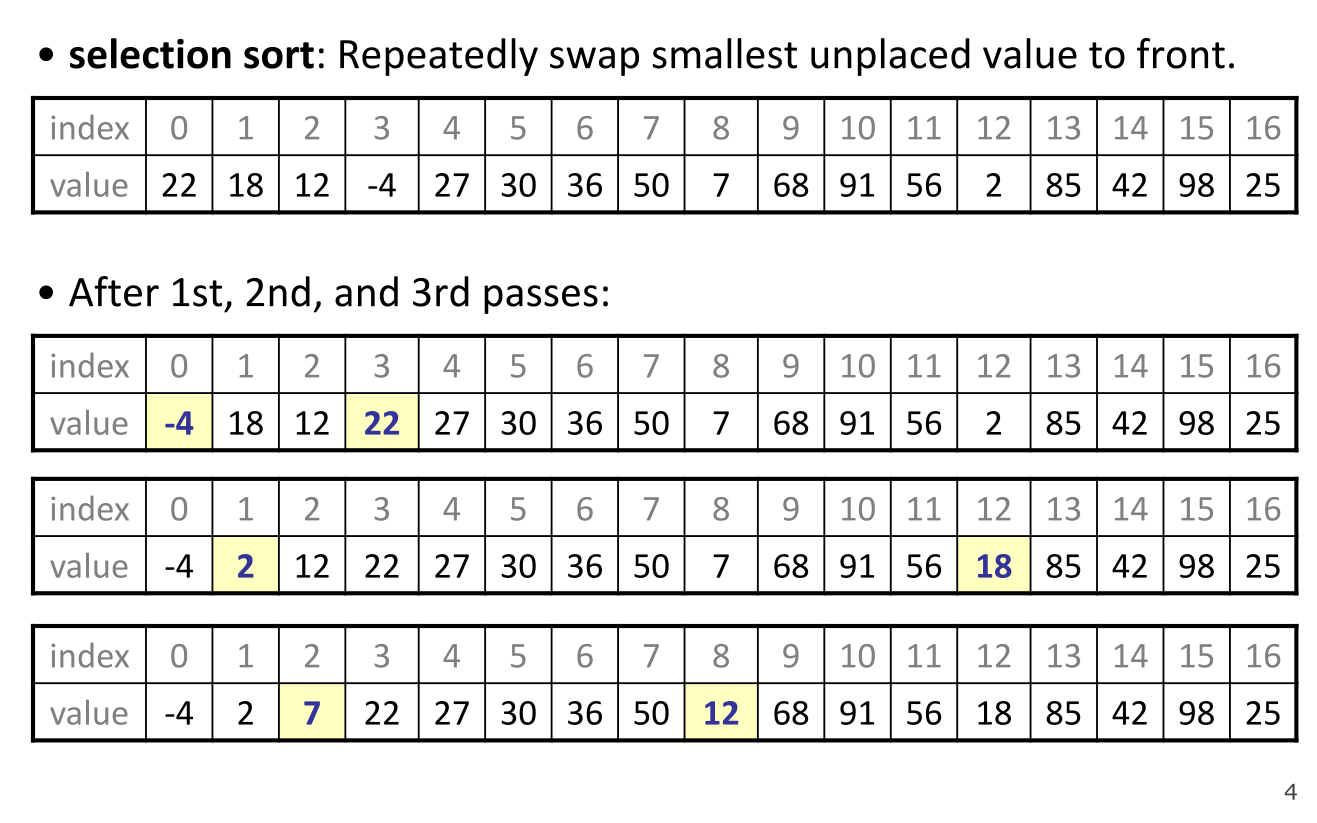
选择排序
相比于其他的算法,选择排序算法更为简单直观,且事件复杂度均是 $O(n^2)$,唯一的好处可能就是不需要占用额外的内存空间。
算法的步骤如下:
- 首先从未排序序列中找到最小(大)元素,存放到排序序列的开始的位置;
- 再从剩余的 未排序中继续寻找,然后放到已排序的序列的末尾;、
- 重复第二步,直至所有元素排序完毕为止。
// Rearranges elements of v into sorted order.
void selectionSort(Vector<int>& v)
{ for (int i = 0; i < v.size() - 1; i++)
{ // find index of smallest remaining value
int min = i;
for (int j = i + 1; j < v.size(); j++)
{ if (v[j] < v[min])
{
min = j;
}
}
// swap smallest value to proper place, v[i]
if (i != min)
{
int temp = v[i];
v[i] = v[min];
v[min] = temp;
}
}
}
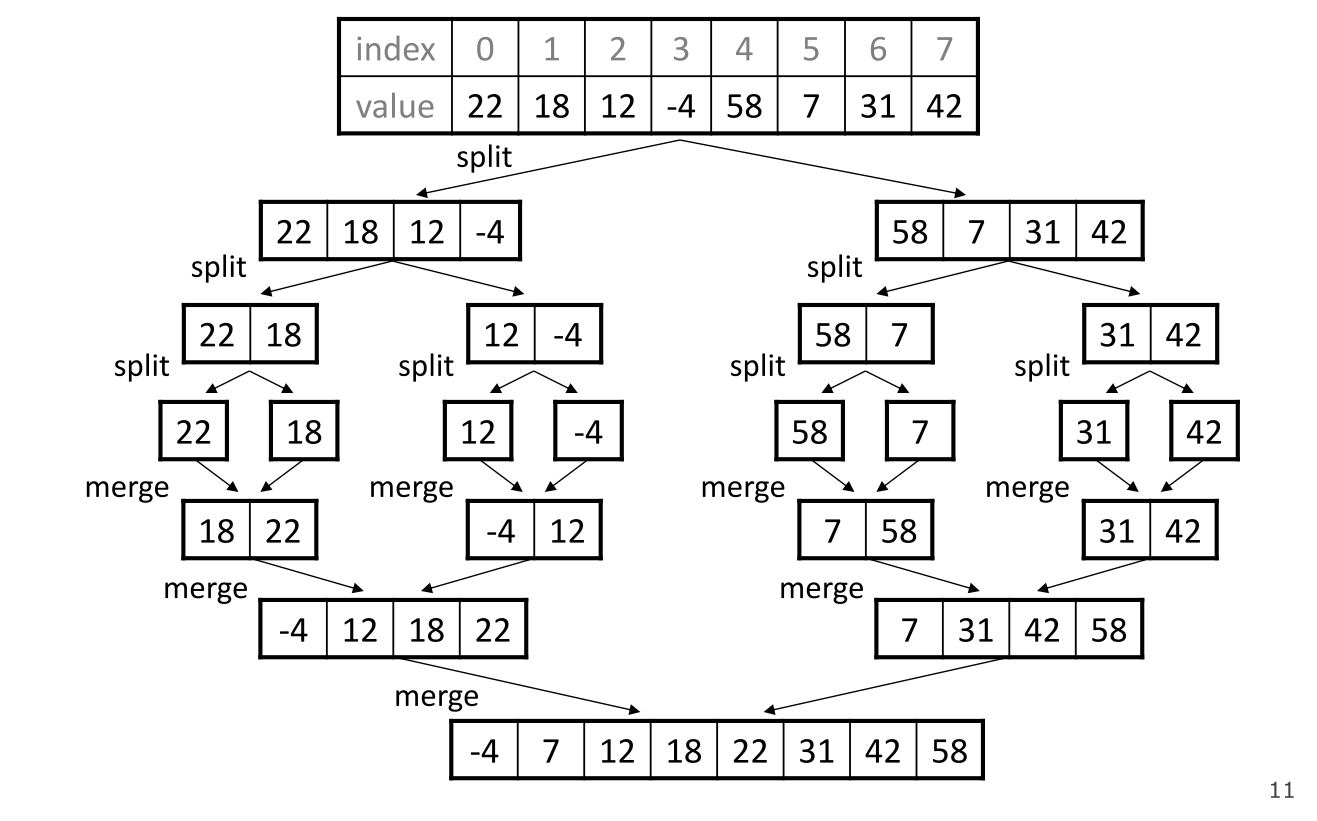
归并排序
归并排序是采用了分治法的一个非常典型的例子。归并排序可以考虑为将数组划分为两半,对两个子序列分别进行排序,对子序列的排序过程也是将其划分(split),直至无法划分时,再将其合并起来(merge),形成一个有序的子序列。
在整个过程中,可以采用递归的方法实现,也可以采用迭代的方式去实现。
算法的步骤如下:
// Rearranges the elements of v into sorted order using
// the merge sort algorithm.
void mergeSort(Vector<int>& v)
{
if (v.size() >= 2)
{
// split vector into two halves
Vector<int> left = v.subList(0, v.size() / 2);
Vector<int> right = v.subList(v.size() / 2 + 1);
// recursively sort the two halves
mergeSort(left);
mergeSort(right);
// merge the sorted halves into a sorted whole
v.clear();
merge(v, left, right);
}
}
// Merges the left/right elements into a sorted result.
// Precondition: left/right are sorted
void merge(Vector<int>& result, Vector<int>& left, Vector<int>& right)
{
int leftIndex = 0;
int rightIndex = 0;
for (int i = 0; i < left.size() + right.size(); i++)
{
if (rightIndex >= right.size() || (leftIndex < left.size() && left[leftIndex] <= right[rightIndex]) )
{
result += left[leftIndex];
// take from left
leftIndex++;
}
else
{
result += right[rightIndex];
// take from right
rightIndex++;
}
}
}
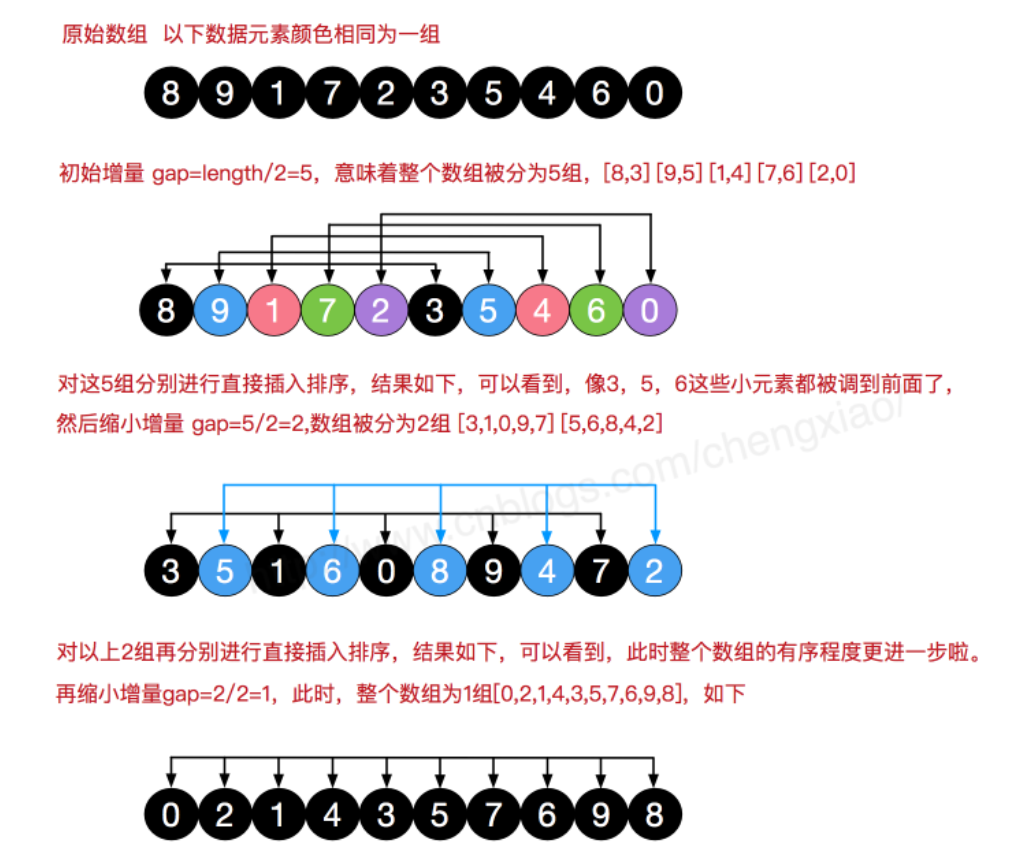
希尔排序
希尔排序,又称为递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序的基本思想是:先将整个待排序的记录序列分割成若干子序列进行插入排序,待整个序列基本有序时,再对全体依次进行插入排序。
算法步骤是:
- 设计一个增量序列 $d_i$,每趟将数据分为 $d_i$ 组,即下标差 $d_i$ 的元素为一组;
- 对各个小组进行插入排序;
- 至最后增量为1时,即是对整个数组进行插入排序。
template<typename T>
void shell_sort(T array[], int length) {
int h = 1;
while (h < length / 3) {
h = 3 * h + 1;
}
while (h >= 1) {
for (int i = h; i < length; i++) {
for (int j = i; j >= h && array[j] < array[j - h]; j -= h) {
std::swap(array[j], array[j - h]);
}
}
h = h / 3;
}
}
堆排序
堆排序指的是利用堆这种数据结构所设计的一种排序算法。堆积时一个近似完全二叉树的结构,并且同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)其父节点。故堆排序又可以分为大顶堆和小顶堆。
算法的步骤如下:
(暂时没看懂,容我先跳过
桶排序
先讲一下桶,每个桶有一定的容量,也就是说每个桶中可能会有多个元素。大体上来说,排序希望数据在桶中的分布比较均匀,即不会出现数据过多或过少的桶。
桶排序的工作原理是将待排序的序列分到若干个桶内,每个桶内的元素再进行个别排序。
在将数据放入桶中时需要注意,要保证右边的桶中的数据比昨天的桶的数据大,这样子在桶内进行排序之后,整体才是一个有序的序列。

import java.util.ArrayList;
import java.util.List;
public class test3 {
public static void main(String[] args) {
int a[]= {1,8,7,44,42,46,38,34,33,17,15,16,27,28,24};
List[] buckets=new ArrayList[5];
for(int i=0;i<buckets.length;i++)//初始化
{
buckets[i]=new ArrayList<Integer>();
}
for(int i=0;i<a.length;i++)//将待排序序列放入对应桶中
{
int index=a[i]/10;//对应的桶号
buckets[index].add(a[i]);
}
for(int i=0;i<buckets.length;i++)//每个桶内进行排序(使用系统自带快排)
{
buckets[i].sort(null);
for(int j=0;j<buckets[i].size();j++)//顺便打印输出
{
System.out.print(buckets[i].get(j)+" ");
}
}
}
}
基数排序
基数排序是一种非比较性整数排序算法,原理是将整数按位数切分成不同的数字,然后按个位数进行比较,同时也可以适用于字符串和特定格式的浮点数。
在进行基数排序时,往往根据确定数据中最大的位数 d,然后根据位数来对每一位进行排序,共总共进行 d次排序。
示例如下:

int maxbit(int data[], int n) //辅助函数,求数据的最大位数
{
int maxData = data[0]; ///< 最大数
/// 先求出最大数,再求其位数,这样有原先依次每个数判断其位数,稍微优化点。
for (int i = 1; i < n; ++i)
{
if (maxData < data[i])
maxData = data[i];
}
int d = 1;
int p = 10;
while (maxData >= p)
{
//p *= 10; // Maybe overflow
maxData /= 10;
++d;
}
return d;
/* int d = 1; //保存最大的位数
int p = 10;
for(int i = 0; i < n; ++i)
{
while(data[i] >= p)
{
p *= 10;
++d;
}
}
return d;*/
}
void radixsort(int data[], int n) //基数排序
{
int d = maxbit(data, n);
int *tmp = new int[n];
int *count = new int[10]; //计数器
int i, j, k;
int radix = 1;
for(i = 1; i <= d; i++) //进行d次排序
{
for(j = 0; j < 10; j++)
count[j] = 0; //每次分配前清空计数器
for(j = 0; j < n; j++)
{
k = (data[j] / radix) % 10; //统计每个桶中的记录数
count[k]++;
}
for(j = 1; j < 10; j++)
count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中
{
k = (data[j] / radix) % 10;
tmp[count[k] - 1] = data[j];
count[k]--;
}
for(j = 0; j < n; j++) //将临时数组的内容复制到data中
data[j] = tmp[j];
radix = radix * 10;
}
delete []tmp;
delete []count;
}
总结