堆

（这节内容并没太多，轻松了~）

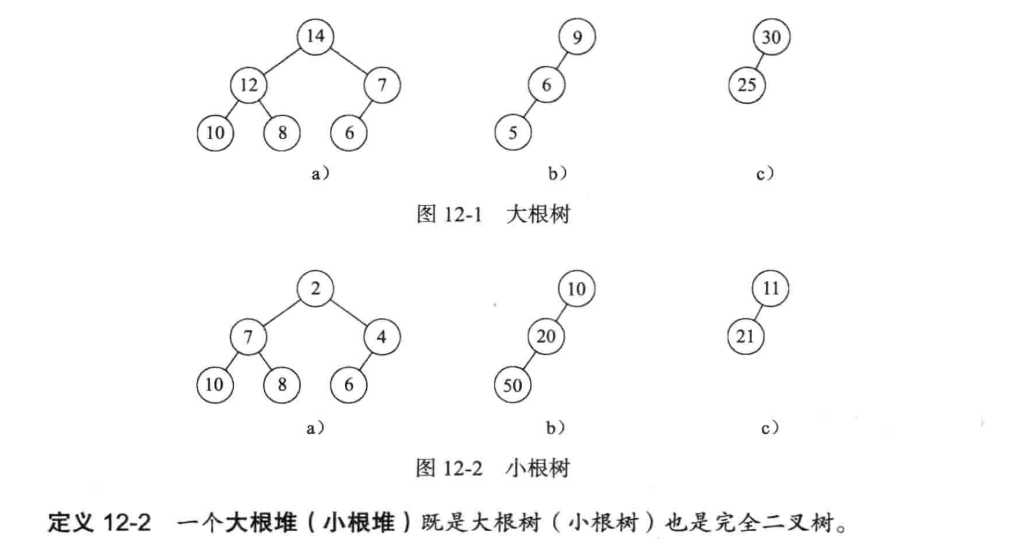
定义

堆是计算机中一类特俗的数据结构，通常可以被看做一颗完全二叉树的数组对象。

一般来说，堆满足下列的性质：

• 堆中的某个结点的值总是不大于或不小于其父节点的值；
• 堆总是一颗完全二叉树。

根据第一点性质，堆可以分为：最大堆（大根堆）和最小堆（小根堆），在最大堆中，父节点的值比任何一个子节点的值都要大，在最小堆中，父节点的值比任何一个子节点的值都要小。

堆的常用方法是：

• 构建优先队列；
• 支持堆排序；
• 快速找出一个集合中的最小值（或是最大值）。

堆和普通树的区别

虽然堆的呈现形式比较像树，但是通常我们都会用数组来进行实现而不是指针。

• 内存占用：普通树占用的内存空间比它们存储的数据要多。因为你要为每个节点的指针分配内存。而堆仅仅使用数组来存储数据，不需要指针。
• 搜索：再二叉树中进行搜索会很快，而堆不适合用于搜索。堆的目的一般是将最大/最小值放在根节点处。

基于数组实现

存储在 T 中位置 P 的元素的索引有函数 f(p)，其定义如下：

• 如果 p 是 T 的根节点，则 f(p) = 0；
• 如果 p 是位置 q 的左孩子，则 f(p) = 2f(q) + 1；
• 如果 p 是位置 q 的有孩子，则 f(p) = 2f(q) + 2。

通过这种方式，就可以将堆中的元素落在$[0, n -1 ]$ 的数组里边。

代码实现如下：

实现优先级队列

增加操作

首先，我们会为了维持完全二叉树的属性，将新节点尽量往靠右靠下的位置放，如果底层的节点已经满了，那么就放在新的一层最左边的位置。

同时，为了保护 heap-order属性，即父节点小于/大于所有子节点，我们会依次进行冒泡操作。将插入节点p与其父节点q进行比较（此处假设是小根堆），若$k_p < k_q$，则将 p 和 q 节点交换位置，而进行了交换操作后，可能会导致上层的 heap-order 属性被破坏，因此需要再进行判断。

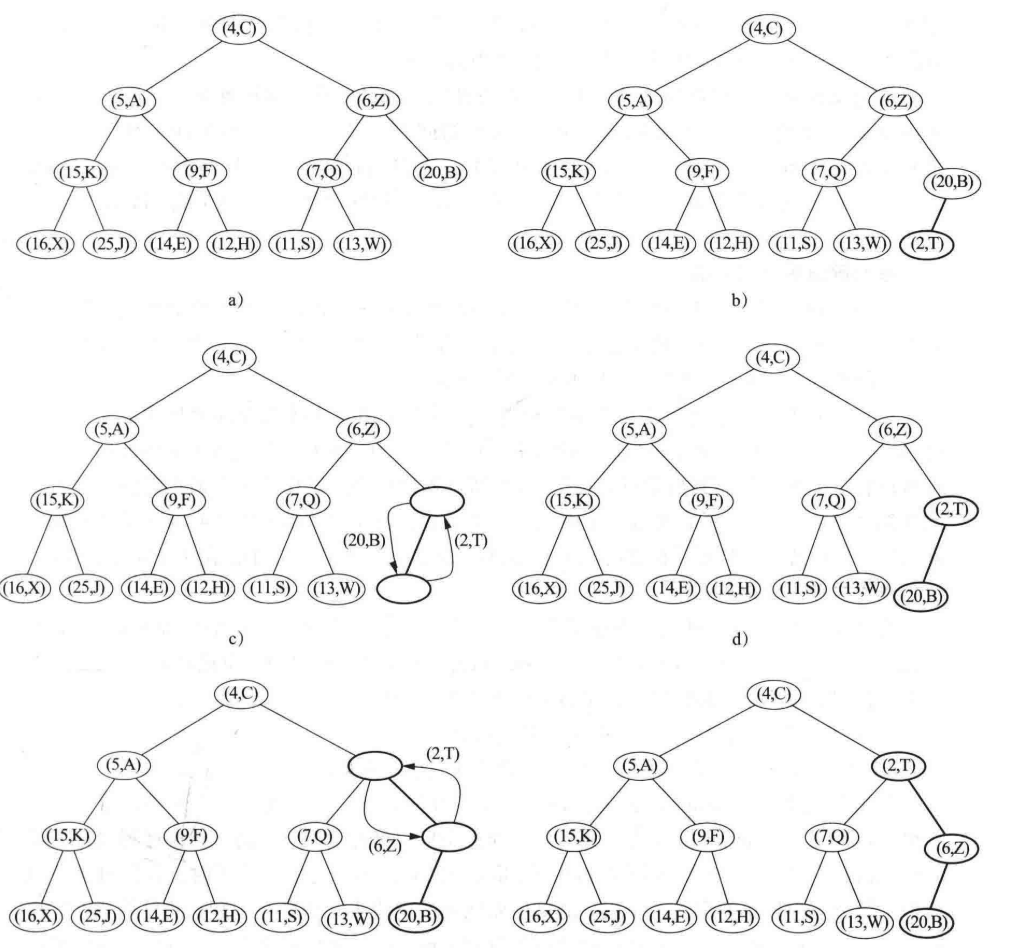
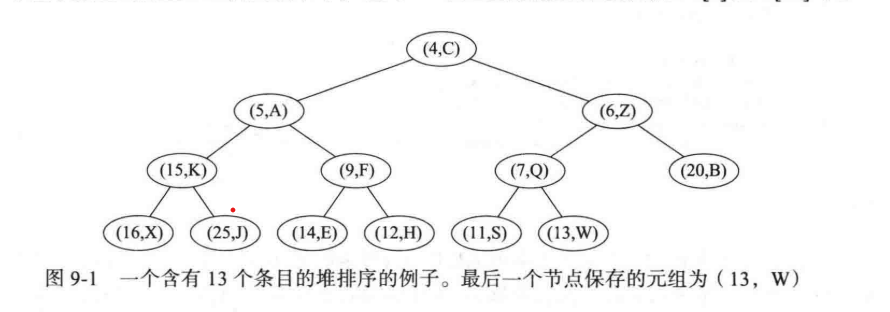
删除键值最小操作

若我们是一个小根堆，一般情况下我们不能简单的删除节点 r，因此此时键值最小的节点存储在根位置，如此操作会产生两颗不相连的子树。

那么我们如何操作的呢？我们将堆最后一个叶子节点给删除，然后将其数值复制到根结点处，再进行如同增加操作中的冒泡操作(增加操作处是向上冒泡，这里是向下冒泡），将堆中最小的元素置换到根节点的位置。

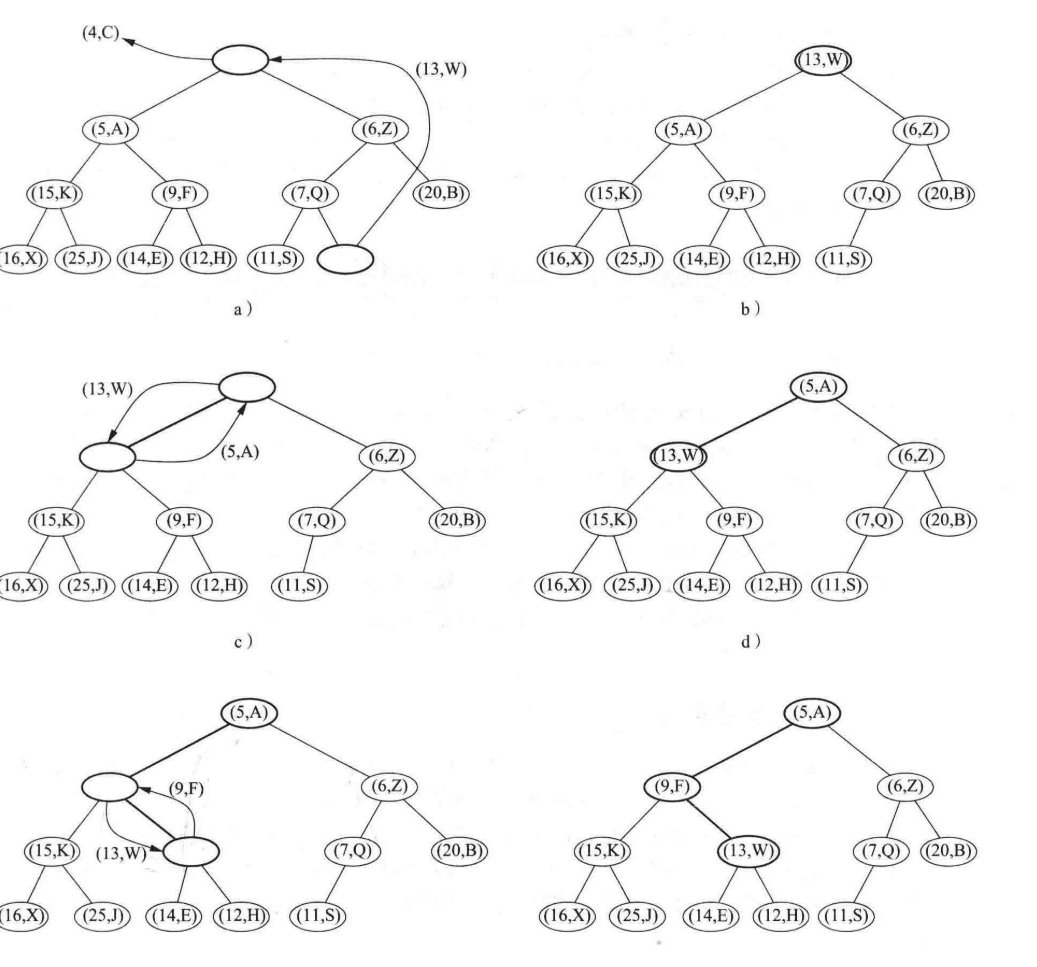
删除任何节点操作

上文处，我们讲了如何删除根节点，那么如何删除堆中的任何一个节点呢？

答案其实是一样的。为了不破坏 heap-order 的属性，在进行删除时，我们同样会删除最后一个节点，然后将其数据拷贝至我们需要删除的那个节点的位置。在这种情况下，我们需要比较拷贝后该节点的数值和其父节点/子节点的数字大小，因为我们不清楚是需要进行向上冒泡操作，还是需要进行向下冒泡操作，但其实过程都并不繁琐。

大根堆的初始化

在很多时候，我们需要将完全二叉树转化成我们需要的数据类型，比如大根堆。进行转化的过程如下：我们首先从最后一个具有孩子的节点还是检查（这点从数组的下标就可以进行判断）。这个元素在数组中的位置是$[n / 2]$。如果以这个元素为根的子树是大根堆，则不做操作；如果以这个元素为根的子树不是大根堆，则必须将其调整为大根堆（冒泡操作）。然后继续检查以$i - 1，i -2 $ 等节点为根的子树，直至检查到以 1 为根的树为止。

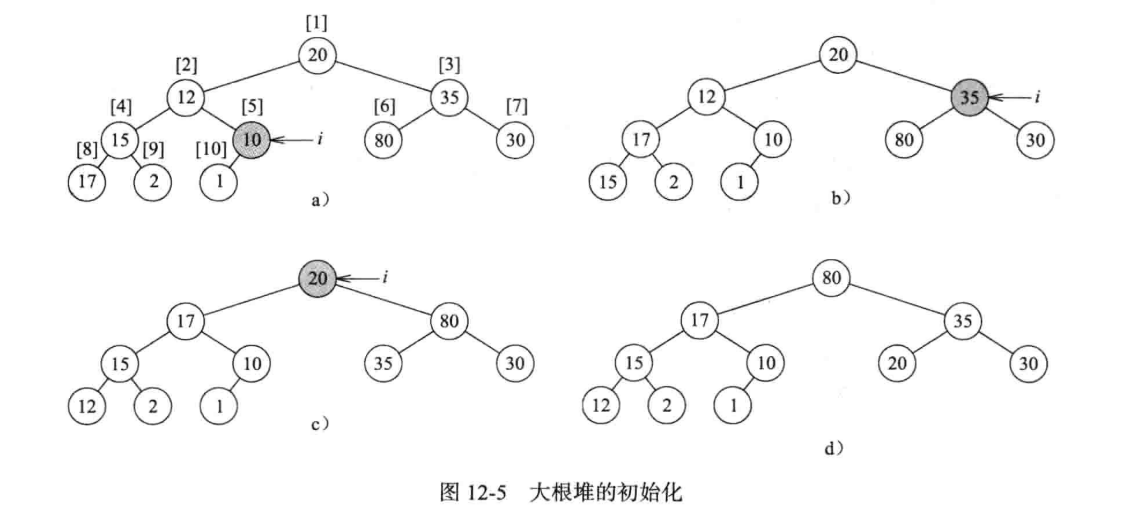
自底向上的堆的构建

（好难咦，学不会