跳跃表(未完)
定义
跳跃表提供一个相当聪明的方式来支持查找和更新操作。一个映射 M 的跳跃表 S 包含一列表序列${S_0, S_1, …,S_n}$ 。每一个列表 $S_i$ 按照键的升序存储着 M 的一个元组子集,用两个标注为 -∞ 和 +∞ 的哨兵追加元组,此外,列表S 还需满足以下的条件:
- 列表$S_0$ 包含映射 M 中的每一项。
- 对于 $i = 1, …, h - 1$,列表 $S_i$ 包括一个列表 $S_{i-1}$ 随机生成的元组的子集。
- 列表 $S_h$ 仅包含 -∞ 和 +∞。
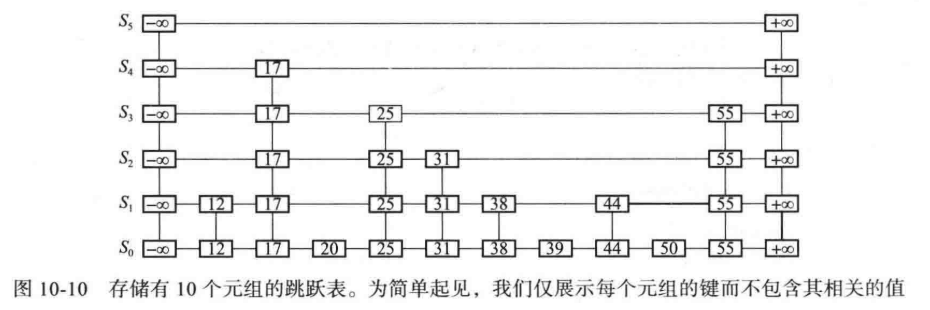
直观的来说, $S_{i = 1}$ 中的元组都是从 $S_i$ 中随机挑选出来的,从 $S_i$ 挑选到 $S_{i + 1}$ 的概率为$1/2$ ,大体上, $S_i$ 中的每一项都是通过类似于“抛硬币”(纯随机)的方式挑选出来的。因此我们希望 $S_1$ 有 $n/2$ 个元组,$S_2$ 有 $n/4$ 个元组,依次类推。
在数据结构和算法设计中使用随机选择主要的优势在于它的结构和函数会变得简单和高效。跳跃表的查找时间和二分查找一样是限定在对数级的范围,在插入和删除元组时,它也扩展了更新算法的性能。
对于跳跃表中,大致存在的操作有下:
| 函数 | 描述 |
|---|---|
| next(p) | 返回在同一水平层位置上 P 下一个位置 |
| prev(p) | 返回在同一水平层位置上在 P 之前的位置 |
| below(p) | 返回在同一垂直塔位置上在 p 下面的位置 |
| above(p) | 返回在同一垂直塔位置上在 p 上面的位置 |
查找操作
,假设要查找键值 K ,进行查找的步骤如下:
- 我们从最左上方的值开始进行查找;
- 对于每一层,我们将 P 向右移动直至它当前位于水平层的最右边的位置;(也有范围限制的噢)
- 如果节点 p 的下方不为空(即 below(p) 不为空),将节点下降一个水平层,重复操作至第二步。


插入操作
在进行插入之前,需要先进行查找操作,即找到应该插入的位置在哪里,因为列表 $S_0$ 是按照升序来进行排列的。在进行查找之后,如果有相同的键值存在,则对其 v 值进行覆盖;若不存在,则我们创建一个垂直塔,并且使用随机方式来决定新元组的垂直塔的高度(抛硬币)。
(注意,上述的查找操作,最后所查到的节点是比要插入键值的位置大那么一丢丢的)

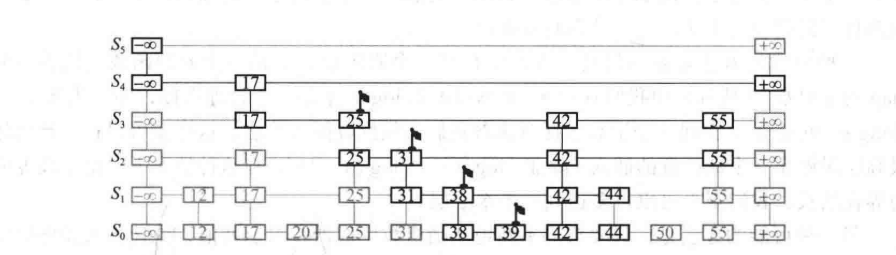
删除操作
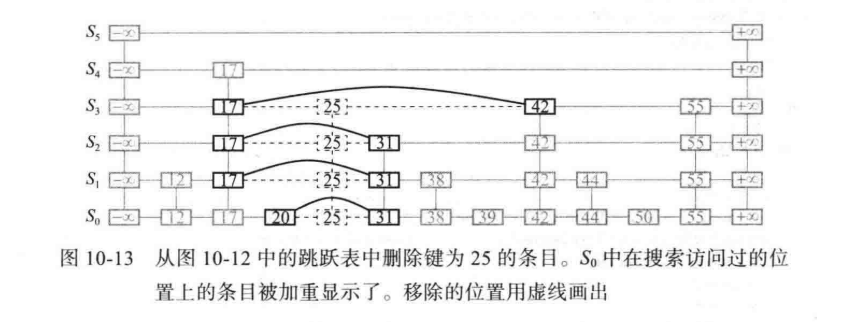
跳跃表中的移除算法和搜索、插入算法是类似的。且事实上,其甚至比插入算法要更加简单。我们首先执行 SkipSearch(k) 查找操作,如果位置 p 存储的条目与键 K 不同,则返回 KeyError。否则,我们移除 p 和 p之上的所有的位置。同时,在移除各层时,要记得重新建立两边邻居之间的链接哦~(不然就找不到彼此了)
维护最高层
对于跳跃表S, 必须维护一个引用初始位置作为实例变量(最左上方的位置),并且应该存在一个策略来阻止任何可能越过顶层高度的插入操作出现。一般来说有两种方法。
- 一种可能的方法是限制最高层 h 保持在某一个固定的数值,$h = max(10, 2,[log n])$ 是一个合理的选择。若通过这个函数来对最高层进行维护的话,意味着我们需要对插入算法进行一定的修改,防止其高度超过最高层 h 的限制。
- 另一种方法是,从头部不断地生成随机数生成器并获得返回值,就让插入操作继续插入新的位置。
跳跃表的操作总结如下:
| 操作 | 运行时间 |
|---|---|
| len(M) | O(1) |
| k in M | 期望为 O(log n) |
| M[k] = v | 期望为 O(log n) |
| del M[k] | 期望为 O(log n) |
| M.find_min(),M.find_max() | O(1) |
| M.find_lt(k), M.find_gt(k) | 期望为 O(log n) |
| M.find_le(k),M.find_ge(k) | 期望为 O(log n) |
| M.find_range(start, stop) | 期望为 O(s + log n) |
| iter(M), reversed(M) | O(n) |
