散列

字典

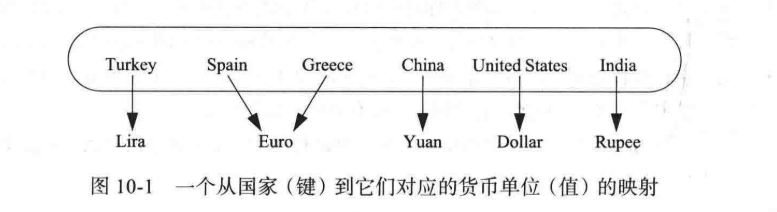
我们首先想想现实中的字典。在现实生活中，当你需要查询一个字时，可以选择通过部首查询，也可以通过拼音查询，这就是索引的不同性；当你通过上述方法进行查询时，拼音/部首 + 页码可以帮助你查找到你想要的字且这个途径是唯一的，也就是说索引和值是一一对应的关系。（即索引是唯一的，而值不是唯一的）

示例如下：

有关字典的操作有：

• 确定字典是否为空；
• 确定字典有多少个数对；
• 寻找一个指定了关键字的数对；
• 插入一个数对；
• 删除一个制定了关键字的数对。

哈希

字典的一种表示方法是散列(hashing)。它用一个散列函数（也成为哈希函数）把字典的数对映射到一个哈希表的具体位置。如果数对 p 的关键字是 k，哈希函数是 f，那么在理想情况下， p 在散列表的位置为 f(k)。

可以理解，线性表也是一种哈希表，不过其对下标没有进行任何处理。

但如果按此来进行设计则会有许多缺点，因为当元素的数目远远大于此时的线性表长度时，我们并不会希望将数组的长度扩展到N；另外，我们一般不会要求一个映射键必须是整数。哈希表的一个概念是使用哈希函数将每个一般的键映射到一个表中的相应索引上。在实际的应用过程当中，可能会存在不同的键被映射到了同一个索引上，这个时候我们就将表化为桶数组，即一个索引处可以存储多个数值对。

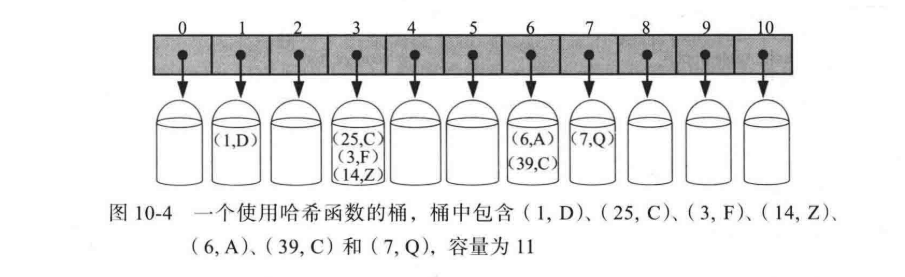
哈希函数

哈希函数 h 的目标就是把每个键映射到 [0, N - 1]区间内的整数，其中 N 是哈希表的桶数组的容量。当两个或者多个键具有相同的哈希值时，那么两个不同的元组将会被映射到相同的桶 A 中。在这种情况下，叫做发生了一次冲突。虽然有很多的方法来解决冲突，但是最好在最初就尽量避免冲突的发生（可以通过巧妙地设置哈希函数达到这个目的）。

评价哈希函数常见的方法由两个部分构成：一个哈希码：将一个键映射到一个整数；一个压缩函数：将哈希码映射到一个桶数组的索引。哈希码的计算部分独立于哈希表的大小，这样子就可以为每一个对象开发一个通用的哈希码，只有压缩函数的设置才与具体的表的大小有关系。

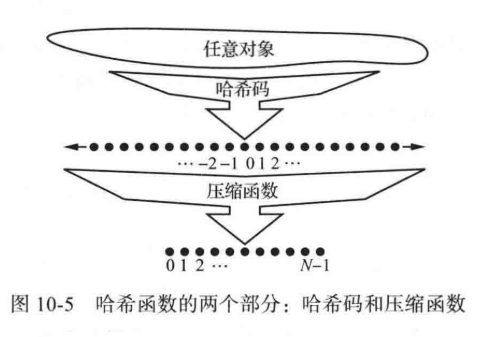
哈希码

哈希函数执行的第一步是取出映射中的任意一个键K，并且计算得到一个整数作为键 K 的哈希码；这个整数不需要在 $[0, N - 1]$范围内，甚至可以是负数。同时，我们希望分配给键的哈希码集合能够尽量的避免冲突。因为如果哈希码发生了冲突，那么压缩函数则无法回避这种冲突。

多项式哈希码

循环移位哈希码

压缩函数

通常来说，键 K 的哈希码不会适合直接使用到桶数组中，因为整数哈希码可能是负的也可能会超过桶数组的容量。因此当我们决定对于一个对象 K 的键使用整数哈希码时，还有个问题就是要把整数映射到$[0, N - 1]$的区间上，这个步骤也称为压缩函数。

划分方法

一个简单的划分方法即是对数取余，即： \(i\ mod\ N\) 在这里 N 是桶数组的大小，是一个固定的正整数。事实上，如果我们把 N 设置为一个素数，那么这个压缩函数会有助于哈希值的分散分布以减少冲突的发生。

MAD方法

MAD方法，即（Multiply-Add-and_Divide）方法，这个方法通过： \([(ai + b) mod\ p]mod\ N\) 来对 i 进行映射，这里 N 是桶数组的大小,p 是比 N 大的素数，a 和 b 是从区间$[0, p - 1]$中任意选择的整数，并且a > 0。

冲突处理

分离链表

处理冲突的一个简单的方法是使每个桶 A[j] 存储其自身的二级容易，用一个很小的 list 来实现是一个不错的选择。

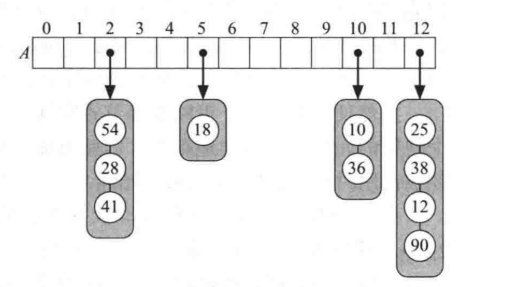
在最坏的情况下，单独的一个桶的操作时间与桶的大小成正比。

开放寻址

如果在某个设备上，空间是一个稀缺资源的话（比如手持设备的小程序），那么我们会采用将每个元组直接存储到一个小的列表插槽中作为替代的方法。由于这种方法没有采用辅助结构，因此也节省了空间，但它需要一个更为复杂的机制来处理冲突，这个方法有几个变种，都统称为开放寻址模式的解决方案。

线性探测及其变种

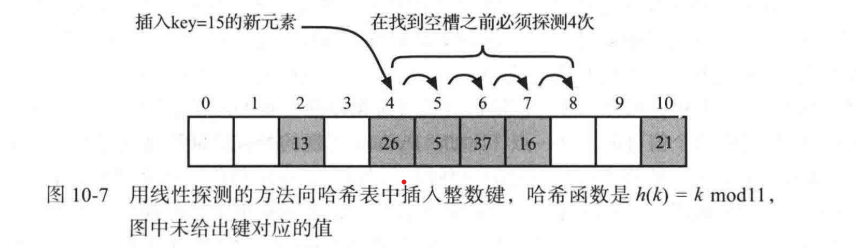
线性探测，说简单一点，就是发现自己的位置被占了之后，向后边依次寻找，如果有空的位置就入座（不是）。线性探测之所以得名，是因为访问桶数组的单元的操作可以被视为“探测”。

需要注意一点的是，若采用线性探测的冲突处理方法，那么在实现删除操作时，就不能把找到的元组简单地从插槽中删除。因为这个位置的元素有可能并不是你想要删除的元素。

负载因子和重新哈希

保证负载因子 $\frac{n}{N}$ 小于 1 是非常重要的，当负载因子的值非常接近 1 时，冲突发生的概率会急剧增加，同时会给我们的操作带来额外开销。

根据实验表明，当使用线性探测的开放寻址策略时，我们应该维持负载因子 < 0.5，而对于其他开放地址策略这个值可能会略微的高一点。

如果一个哈希表的插入操作引起的负载因子超过了指定的阈值，那么调整表的大小（通过改变N 来重新获取指定的负载因子）并且将所有的对象重新插入新表是非常常见的现象。这个操作就叫做重新哈希（Rehashing）。虽然我们不需要再为每个对象重新定义一个新的哈希码，但是我们需要基于新的哈希表大小重新设计一个压缩函数，使得重新哈希将元组分布再整个新的桶数组上。

事实上，如果我们每次重新哈希时总是把表格的大小设置为原来的两倍，那么我们将分期承担重新哈希表格中所有元组的开销，而不是在最初插入这些元组时一次性全部承担。

哈希表的实现