图
图是一种用于表示对象之间的存在关系的方式。即图是对象的一个集合。
定义
(复杂的概念你给我好好记住!
图是有限集 V 和 E 的有序对,即 G = (V, E),其中 V 的元素被称为顶点(也称节点或点),E 的元素称为边(也称弧或线)。对于边,有些边是带方向的,有些边是不带方向的。故图也可区分为:
- 有向图:其中的边都具有方向, (u, v) 和 (v, u ) 不同。
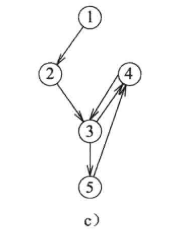
- 无向图:其中的边都没有方向, (u, v) 和 (v, u) 相同。
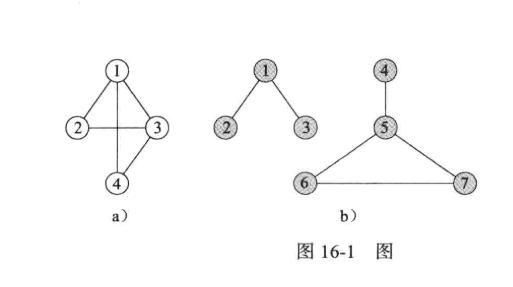

当且仅当 (i, j) 是图的边,称顶点 i 和 j 是邻接的。边 (i, j ) 关联与顶点 (i, j)。
对于有向图当中,定义更加精确。有向边 (i, j) 是关联至顶点 j 而关联于顶点 i ,顶点 i 邻接至顶点 j。
在图的一些应用当中,我们可能需要为每条边赋予一个表示成本的值(可将原有的值看作1),我们称之为权。这样的图称为加权有向图和加权无向图。一个网络经常指一个加权有向图和加权无向图。
简单路径:一个路径,如果除第一个和最后一个顶点之外,其余所有顶点均不同,那么该路径称为一条简单路径。
图或有向图中的每一条边都可以有长度,一条路径的长足则是该路径中所有边的长度之和。
- 连通图:G连通的当且仅当每一对顶点之间都有一条路径。
- 非连通图:存在两个顶点之间未被联通。
子图:如果 H 的顶点和边的集合分别是 G 的顶点和边的集合的子集,那么称图 H 是 G的子图。
环路:一条始点和终点相同的简单路径称为环路。
生成树:一个G 的子图,如果包含 G 的所有顶点,且是一棵树,则称为 G 的生成树。
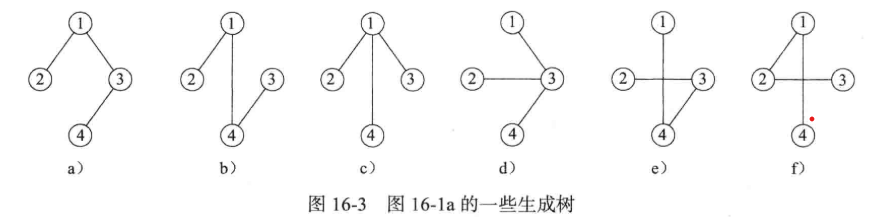
度:在一个无向图中,与一个顶点 i 相关联的边数称为该顶点的度。若G是有向图,则顶点 i 的入度是关联至该顶点的边数(指向它),顶点 i 的初读是指关联于该顶点的边数(指出)。
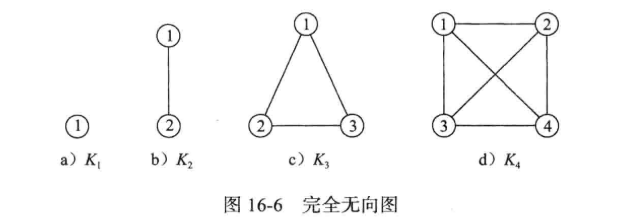
完全图:一个具有 n 个顶点和 n(n - 1 )/ 2 条边的无向图是一个完全图,有 n 个顶点的有向图有 n(n - 1) 条边,则此图为完全有向图。
强连通:一个有向图是强连通的,当且仅当对于每一对不同顶点 i 和 j,从 i 到 j 和从 j 到 i 都有一条有向路径。非强连通图的极大强连通子图被叫做强连通分量。
图的特性
-
设 G = (V, E) 是一个无向图,令 n = V ,e = E ,则: - $\sum_{i = 1}^{n}d_i = 2e$;
- $0 <= e <= n(n - 1) / 2$。
(在无向图中,每一条边都与 2 个顶点相关联,因此顶点的度之和是边数的两倍。一个顶点的度在0 到 n - 1 之间,因此度的和在 0 到 n(n - 1)之间)
-
设 G = (V, E )是一个有向图,令 n = V ,e = E ,则: - $0 <= e <= n(n - 1)$;
- $\sum_{i = 1}^{n}d_i^{in} = \sum_{i = 1}^{n}d_i^{out} = e$。
ADT
对于一个图,应该具备以下的操作:
| functions | description |
|---|---|
| vertex_count() | 返回图中的顶点的数目 |
| vertices() | 迭代返回图中的所有顶点 |
| edge_count() | 返回图中的边的数目 |
| edges() | 迭代返回图中的所有边 |
| get_edge(u, v) | 返回从顶点u到顶点v的边,如果不存在则返回None;对于无向图,get_edge(u, v)和get_edge(v, u) 之间没有区别 |
| degree(v, out = True) | 对于一个无向图,返回其他边入射到 v 的数目。对于一个有向图,返回入射到顶点 v 的输出边的数目 |
| incident_edges(v, out = True) | 返回所有边入射到顶点 v 的迭代循环。在有向图的情况下,默认是输出边。 |
| insert_vertex(x = None) | 创建和返回一个新的存储元素 x 的 vertex |
| insert_edge(u, v, x = None) | 创建和返回一个新的从顶点 u 到顶点 v 的存储元素 x 的 Edge. |
| functions | description |
|---|---|
| remove_vertex(v) | 移除顶点 v 和图中它的所有入射边 |
| remove_edge(e) | 移除图中的边 e |

图的存储表示
无权图的表示
邻接矩阵
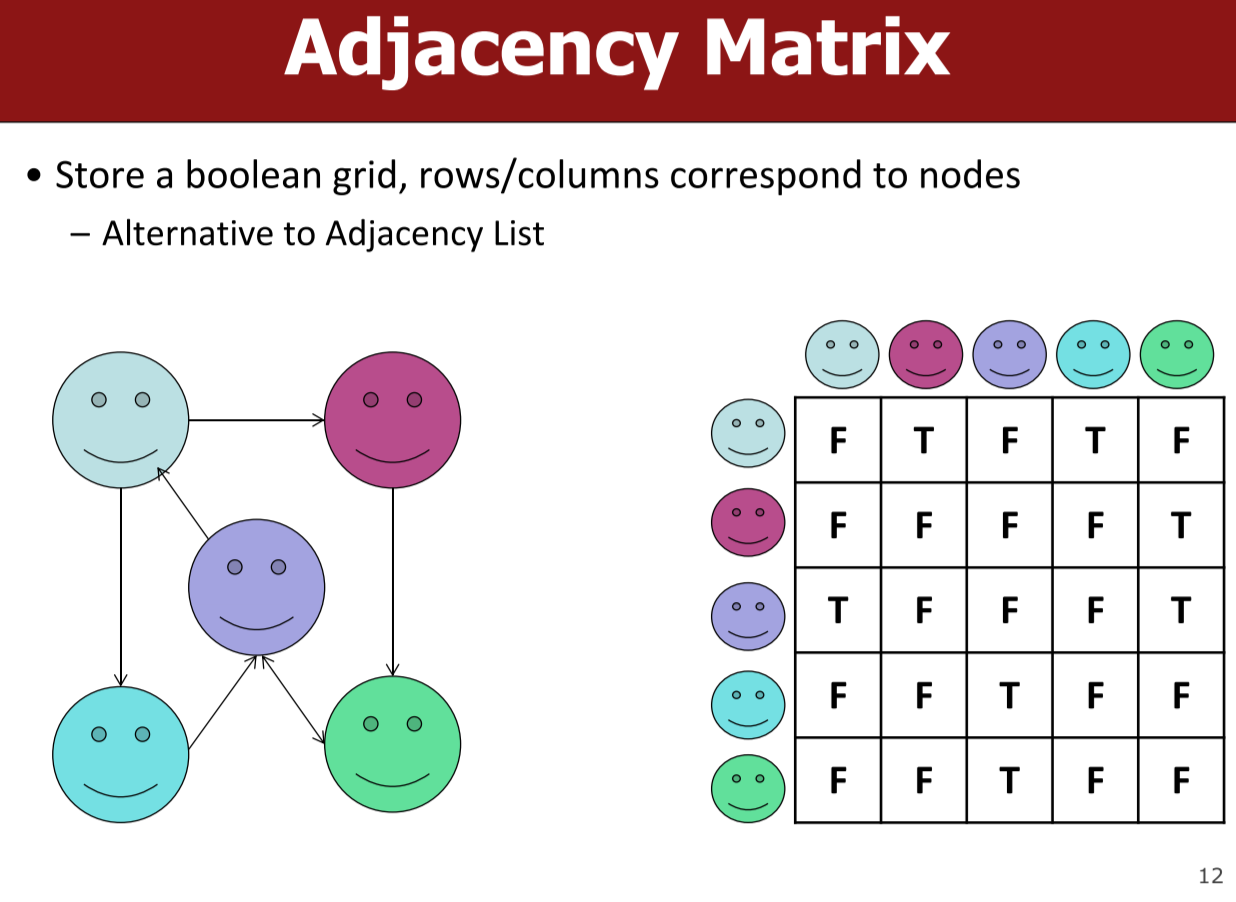
一个 n 顶点图 G = (V, E) 的邻接矩阵(adjacent matrix) 是一个 n x n 的矩阵,其中每个元素是0 或1。如果 G 是无向图,那么其中的元素定义如下:
- A(i, j) = 1,如果 $(i, j )∈ E 或 (j, i) ∈ E$;
- A(i, j) = 0,其他。
如果 G 是有向图,那么其中的元素定义如下:
- A(i, j) = 1,如果$(i, j )∈ E$ ;
- 0,其他。

由上述定义中的描述,我们可以有如下的描述:
- 对于 n 个顶点的无向图,有 $A(i, i) = 0,即对角线上的值为0$;
- 无向图的邻接矩阵是对称的,即$A(i, j) = A(j, i)$,根据这个特性,在存储无向图时,可以选择一种更加节约空间的方法。
- 对于 n 个顶点的有向图,有$\sum_{j = 1}^{n}A(i, j) = d_i^{out}$ 和 $\sum_{j = 1}^{n}A(j, i) = d_i^{in}$。
在存储时,可以把 n x n 邻接矩阵A 映射到一个 $(n + 1) * (n + 1)$ 的布尔型数组,因为所有的对角线元素都是零而不需要存储,所以可以进一步的减少 n 字节的存储空间。把对角线元素去掉,即可以得到一个上/下三角矩阵,这些三角矩阵可以压缩到一个 $(n - 1) * n$ 的矩阵中。
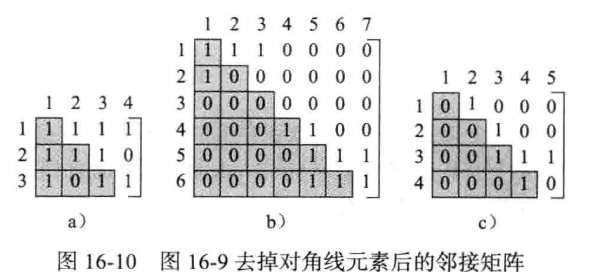
然而,上述方法虽然减少了部分的存储空间,但是却付出了不少代价,因为顶点的外部索引和在图中的内部描述不一致。如此,代码的访问容易出错,且访问边的时间也会增加。
typedef struct
{ int no;
InfoType info;
}VertexTtype
typedef struct
{ int edges[MAXV][MAXV]; /*各顶点之间的关系或权值*/
int n,e; /*顶点数,边(或弧)的个数*/
VertexType vexs[MAXV]; /*存储顶点元素*/
}MGraph;
邻接表/邻接链表
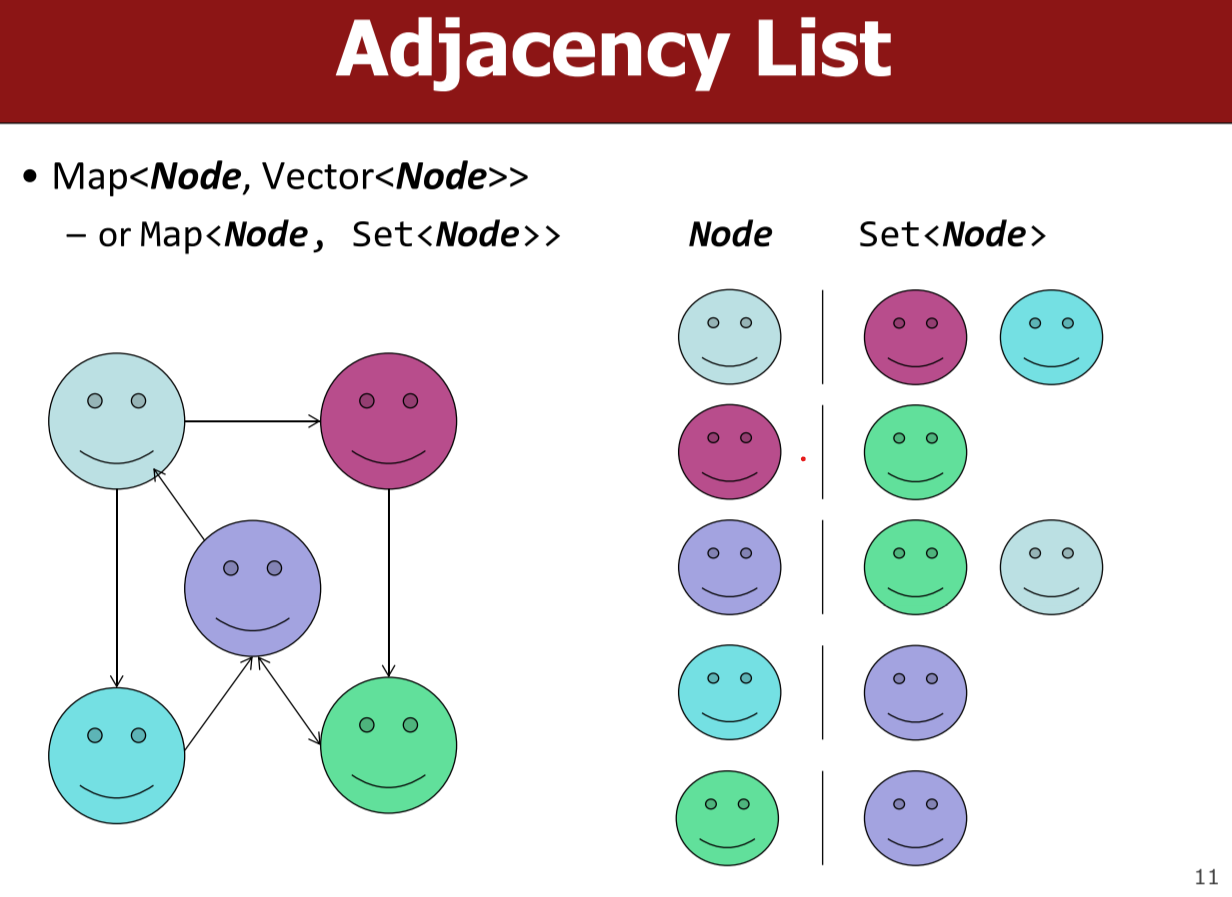
在一个图的邻接表描述当中,图的每一个顶点都有一个邻接表。当邻接表用链表表示时,就是邻接链表(liked-adjacency-list)。
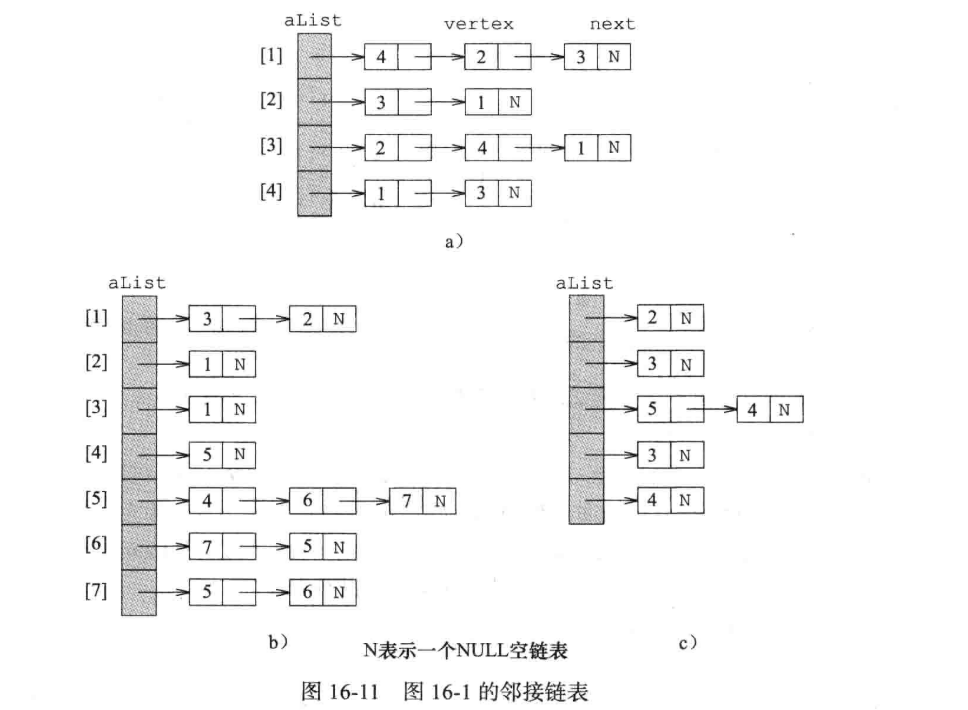
一个指针和一个整数各需要 4 字节的存储空间,因此用邻接链表描述一个 n 顶点图需要 8(n + 1)字节来存储 n + 1 个 firstNode 指针和 listSize 域,需要 4 * 2 * m 字节来存储 m 个链表节点。

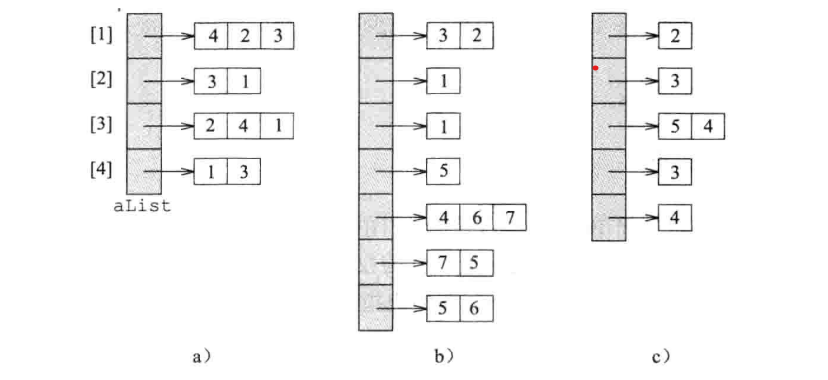
邻接数组
在邻接数组中,每一个邻接表用一个数组线性表而非链表来描述。可以选择的是每个节点后连接一个数组线性表。另一个选择是使用二位不规则数组,其中 aList[i] 容量等于顶点 i 的邻接表长度。 邻接数组必邻接链表少用了 4m 字节,因为不需要 next 指针域。而对于大部分的图操作,无论是用邻接链表,还是用邻接数组,其渐近时间复杂度是相同的。
十字链表
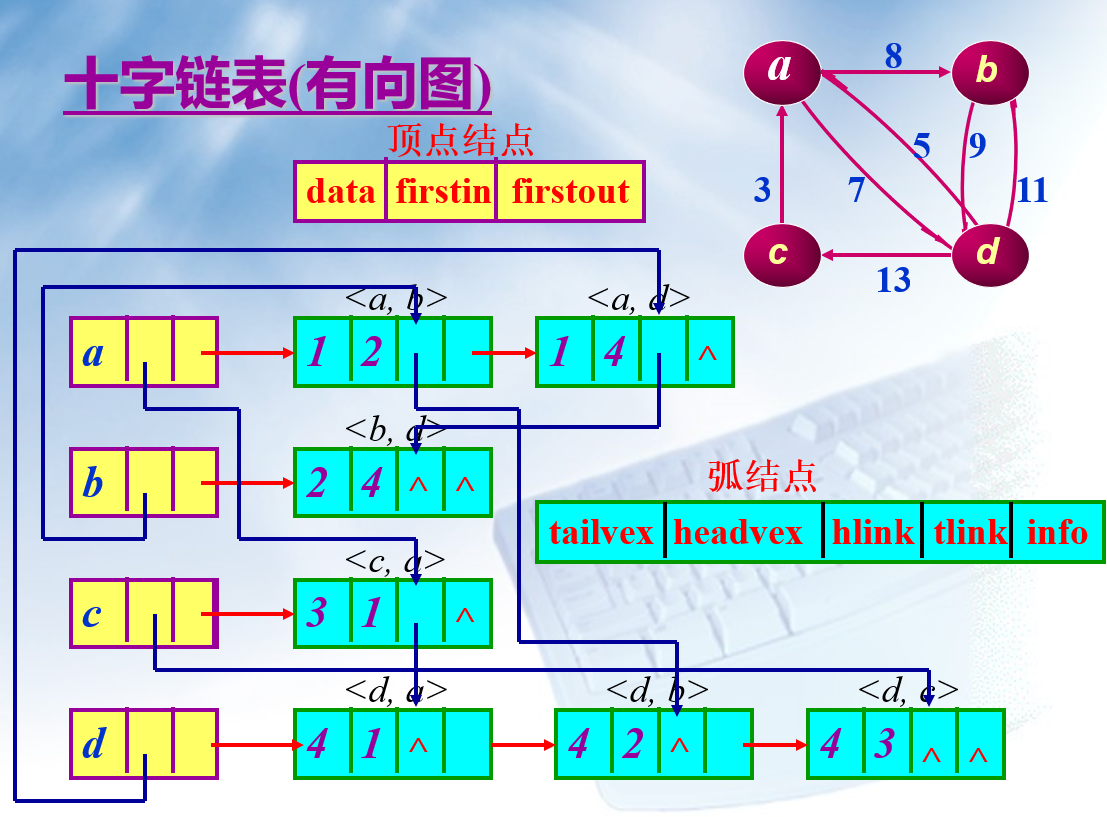
有邻接表不同,十字链表法适用于存储有向图(当然无向图也有对应的存储方法)。
所谓十字链表,就是各个链表相互串联,错综复杂。那么将各个节点和链表连接起来的就是图中的顶点之间的关系。
首节点:

首节点中有一个数据域和两个指针域:
- fisrtin 指针用于连接以当前顶点为弧头的其他顶点构成的链表;
- firstout 指针用于连接以当前顶点为狐尾的其他顶点构成的链表;
- data 用于存储该顶点上的数据。
普通节点:

- tailvex 用于存储以首元节点为弧尾的顶点位于数组中的位置下标;
- headvex 用于存储以首元节点为弧头的顶点位于数组中的位置下标;
- hlink 指针:用于链接下一个存储以首元节点为弧头的顶点的节点;
- tlink 指针:用于链接下一个存储以首元节点为弧尾的顶点的节点;
- info 指针:用于存储与该顶点相关的信息,例如量顶点之间的权值;
#define MAX_VERTEX_NUM 20
#define InfoType int//图中弧包含信息的数据类型
#define VertexType int
typedef struct ArcBox{
int tailvex,headvex;//弧尾、弧头对应顶点在数组中的位置下标
struct ArcBox *hlik,*tlink;//分别指向弧头相同和弧尾相同的下一个弧
InfoType *info;//存储弧相关信息的指针
}ArcBox;
typedef struct VexNode{
VertexType data;//顶点的数据域
ArcBox *firstin,*firstout;//指向以该顶点为弧头和弧尾的链表首个结点
}VexNode;
typedef struct {
VexNode xlist[MAX_VERTEX_NUM];//存储顶点的一维数组
int vexnum,arcnum;//记录图的顶点数和弧数
}OLGraph;
int LocateVex(OLGraph * G,VertexType v){
int i=0;
//遍历一维数组,找到变量v
for (; i<G->vexnum; i++) {
if (G->xlist[i].data==v) {
break;
}
}
//如果找不到,输出提示语句,返回 -1
if (i>G->vexnum) {
printf("no such vertex.\n");
return -1;
}
return i;
}
//构建十字链表函数
void CreateDG(OLGraph *G){
//输入有向图的顶点数和弧数
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
//使用一维数组存储顶点数据,初始化指针域为NULL
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->xlist[i].data));
G->xlist[i].firstin=NULL;
G->xlist[i].firstout=NULL;
}
//构建十字链表
for (int k=0;k<G->arcnum; k++) {
int v1,v2;
scanf("%d,%d",&v1,&v2);
//确定v1、v2在数组中的位置下标
int i=LocateVex(G, v1);
int j=LocateVex(G, v2);
//建立弧的结点
ArcBox * p=(ArcBox*)malloc(sizeof(ArcBox));
p->tailvex=i;
p->headvex=j;
//采用头插法插入新的p结点
p->hlik=G->xlist[j].firstin;
p->tlink=G->xlist[i].firstout;
G->xlist[j].firstin=G->xlist[i].firstout=p;
}
}
有权图的表示
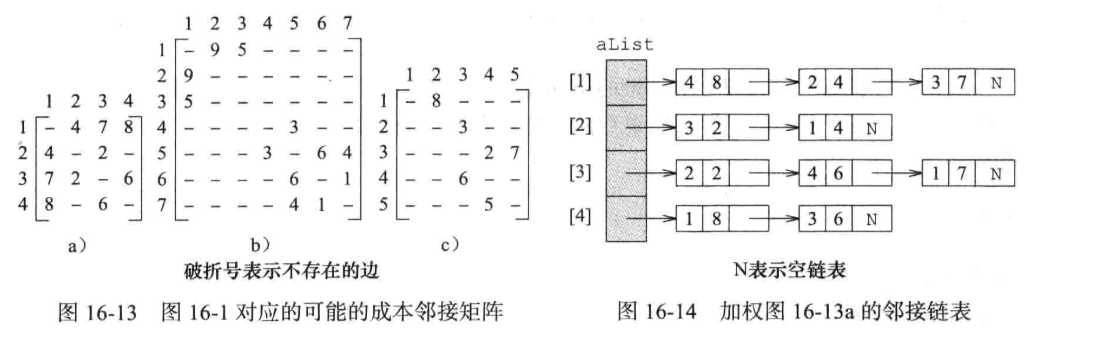
对于有权图,唯一改变的就是边具有了权值,因此将无权图的描述进行简单的扩充(节点域)就可以得到加权图的描述。
成本邻接矩阵
图的遍历
深度优先搜索(DFS)
(老生常谈了,贴个图就行了

广度优先搜索(BFS)

最小生成树
要想了解最小生成树,先要知道什么是生成树:
定义:一个连通图的生成树是一个极小的连通子图,它包含着图中全部的 n 个节点,但只有构成树的 n - 1 条边。
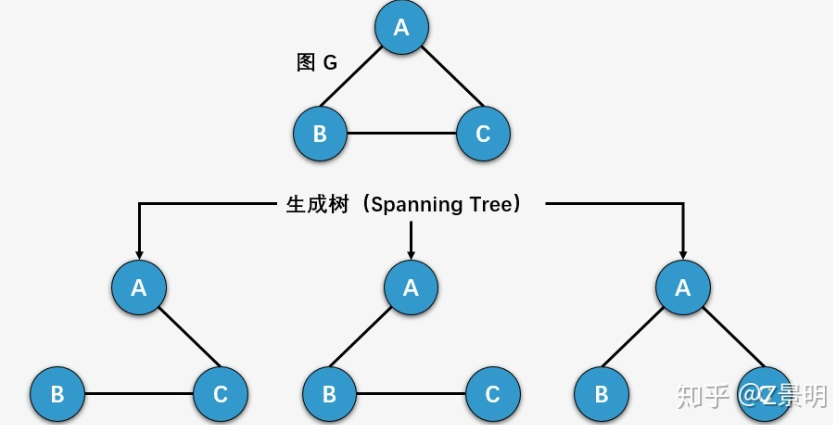
最小生成树:一个带权图的最小生成树,就是原图中边的权值的和最小的生成树。
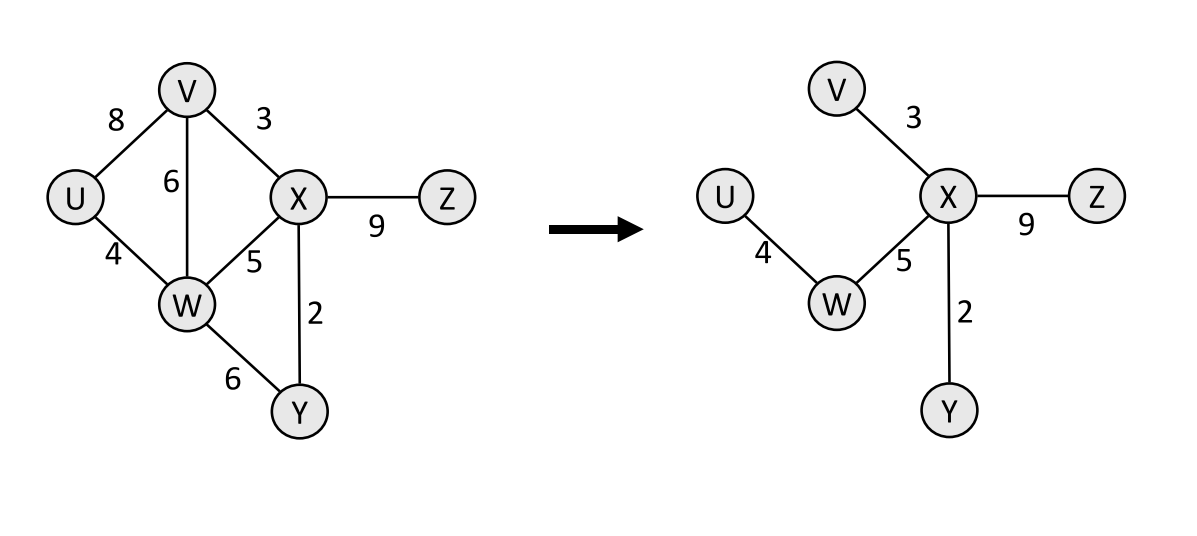
我们下文要讲的 Prim 算法和 Kruskal 算法,均是求解最小生成树的方法。
Prim 算法
Prim 角度主要从点来出发,其将点划分为2类,已经使用过的和未使用过的。
算法大致步骤如下:
- 选取一个初始节点,将其添加至 MST 中;
- 找到MST 中所有元素的相邻的节点,并选取其中权值最小的那个节点;
- 重复上述的第二个步骤,直至所有的节点都被选取。

#define MAX 100000
#define VNUM 10+1 //这里没有ID为0的点,so id号范围1~10
int edge[VNUM][VNUM]={/*输入的邻接矩阵*/};
int lowcost[VNUM]={0}; //记录Vnew中每个点到V中邻接点的最短边
int addvnew[VNUM]; //标记某点是否加入Vnew
int adjecent[VNUM]={0}; //记录V中与Vnew最邻近的点
void prim(int start)
{
int sumweight=0;
int i,j,k=0;
for(i=1;i<VNUM;i++) //顶点是从1开始
{
lowcost[i]=edge[start][i];
addvnew[i]=-1; //将所有点至于Vnew之外,V之内,这里只要对应的为-1,就表示在Vnew之外
}
addvnew[start]=0; //将起始点start加入Vnew
adjecent[start]=start;
for(i=1;i<VNUM-1;i++)
{
int min=MAX;
int v=-1;
for(j=1;j<VNUM;j++)
{
if(addvnew[j]!=-1&&lowcost[j]<min) //在Vnew之外寻找最短路径
{
min=lowcost[j];
v=j;
}
}
if(v!=-1)
{
printf("%d %d %d\n",adjecent[v],v,lowcost[v]);
addvnew[v]=0; //将v加Vnew中
sumweight+=lowcost[v]; //计算路径长度之和
for(j=1;j<VNUM;j++)
{
if(addvnew[j]==-1&&edge[v][j]<lowcost[j])
{
lowcost[j]=edge[v][j]; //此时v点加入Vnew 需要更新lowcost
adjecent[j]=v;
}
}
}
}
printf("the minmum weight is %d",sumweight);
}
Kruskal 算法
相对于 Prim 算法, Kruskal 算法要更加”高级“一点。
定义:Start with an empty structure for the MST Place all edges into a priority queue based on their weight (cost). While the priority queue is not empty: Dequeue an edge e from the priority queue. If e’s endpoints aren’t already connected, add that edge into the MST. Otherwise, skip the edge.
简单描述就是:
- 将所有边的权值添加到一个优先队列当中;
- 从小到大依次进行选择,若该选择会导致环的产生,则舍弃;
- 重复上述步骤,直至满足最小生成树的边的条件。
(ps: 在判断环的产生时,可以判断其是否能回到自己)

Dijkstra 算法
定义:consider every vertex to have a cost of infinity, except v1 which has a cost of 0. create a priority queue of vertexes, ordered by cost, storing only v1 . while the pqueue is not empty: dequeue a vertex v from the pqueue, and mark it as visited. for each unvisited neighbor, n, of v, we can reach n with a total cost of (v’s cost + the weight of the edge from v to n). if this cost is cheaper than n’s current cost, we should enqueue the neighbor n to the pqueue with this new cost, and remember v was its previous vertex. when we are done, we can reconstruct the path from v2 back to v1 by following the path of previous vertices.
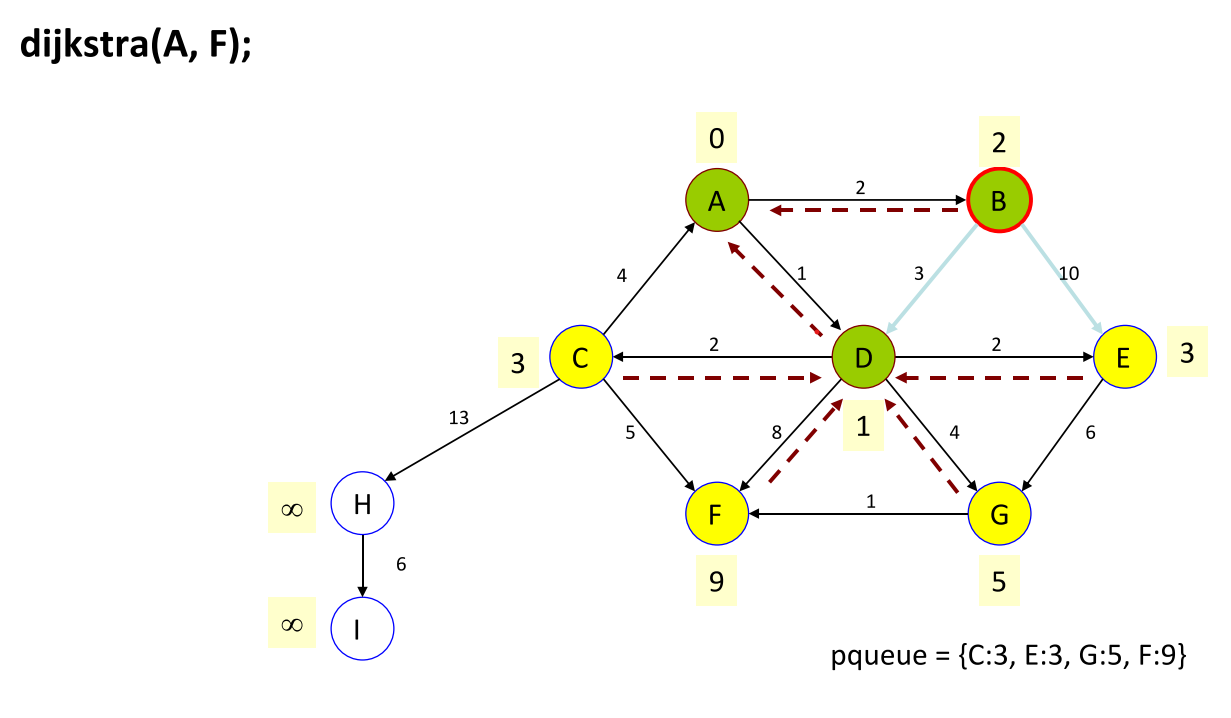
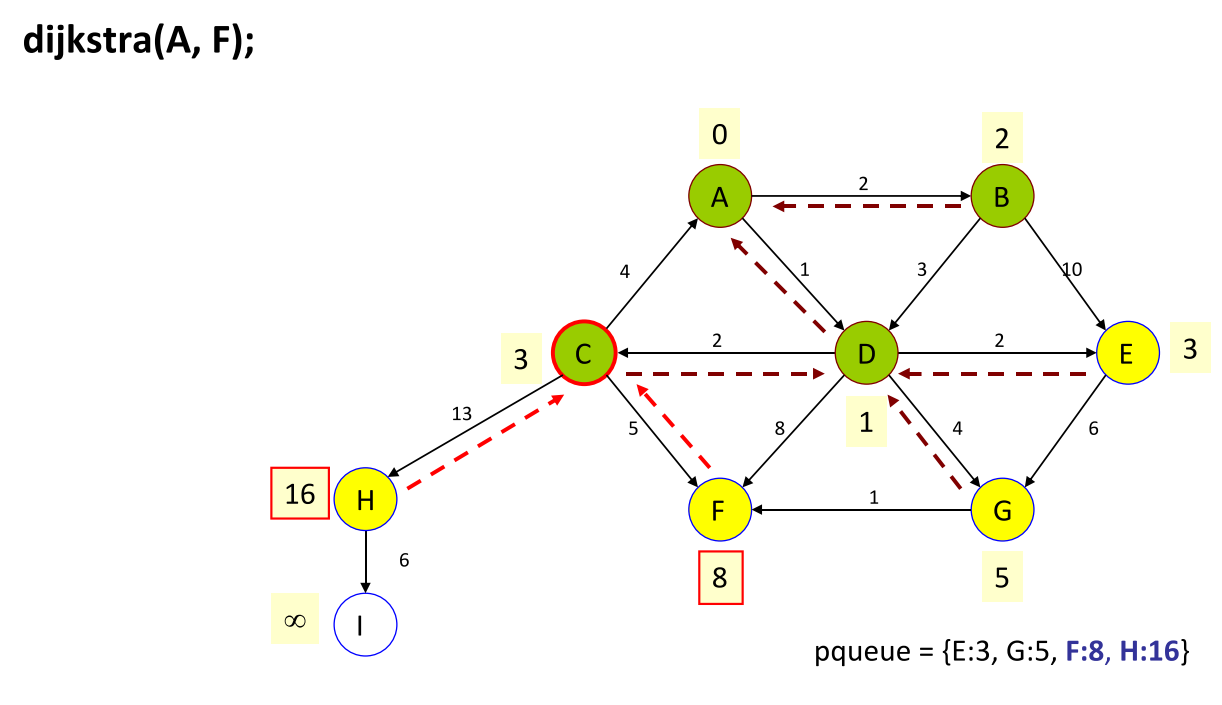
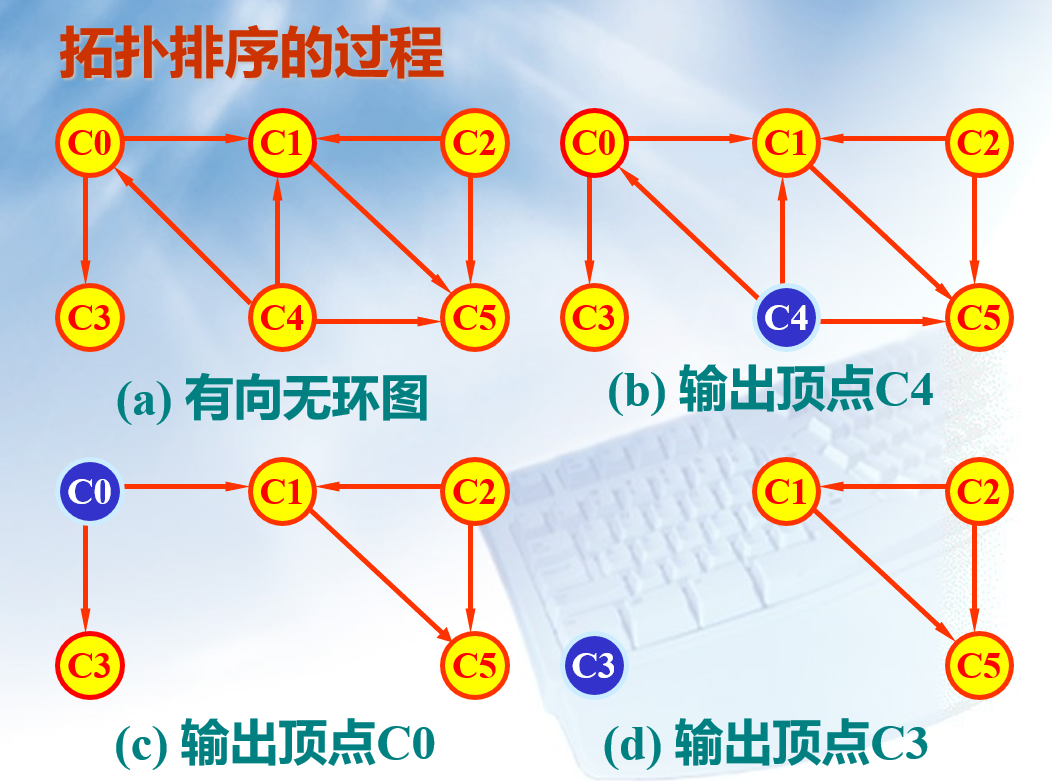
拓扑排序