树
前面所学的线性表,链表,数组之类的均是线性的数据结构,而树则是一个非常重要的非线性数据结构。由于其结构类似于一个倒置的树,故得此名。同时,在描述节点之间的关系的时候,主要术语来源于家谱,例如双亲,孩子等。
定义
通常我们将树 T 定义为存储一系列元素的有限节点集合,这些节点具有 parent-children 关系并且满足以下的属性:
- 如果树 T 不为空,则其一定具有一个称为根节点的特殊节点,并且该节点没有父节点。
- 每个非根节点 V 都具有唯一的父节点 W,每个具有父节点 W 的节点都是节点 W 的一个孩子。
级:树中一个常用的术语是级(level),树根是一级,树根的孩子是二级,孩子的孩子是三级,……。
度:一个元素的度是指其孩子的个数,叶结点的度为 0,一棵树的度是其元素的度的最大值。
边:
ADT
若用位置信息来存储元素,则一棵树的位置对象大至应支持如下方法:
| 方法 | 描述 |
|---|---|
| p.element() | 返回存储在位置 p 的元素 |
| T.root() | 返回树 T 的根节点的位置。若树为空,则返回 None |
| T.is_root(p) | 如果位置 p 是树 T 的根,则返回 True |
| T.parent(p) | 返回位置为 p 的父节点的位置,若 p 是根节点,则返回 None |
| T.num_children(p) | 返回位置为 p 的孩子节点的编号 |
| T.children(p) | 产生位置为 p 的孩子节点的一个迭代 |
| T.is_leaf(p) | 如果位置节点 p 没有任何孩子,则返回 True |
| len(T) | 返回树 T 所包含的元素的个数 |
| T.is_empty() | 如果树 T 不包含任何位置,则返回 True |
深度和高度计算
(注意定义,某些时候会将根的深度定义为0,某些时候会将根的深度定义为1。同时,个人觉得现在对于高度的定义存在一定的混淆,某些教材会将高度和深度划等号,而某些则是完全不同的两个定义。接下来下文的定义采用的是教材《数据结构与算法 python 实现》)
深度:深度的递归定义如下:
- 如果 p 是根节点,那么 p 的深度是0。
- 否则,P 的深度就是其父节点的深度加1。

对于节点 p,方法 T.depth(p) 的运行时间是 $O(d_p + 1)$。
高度:树 T 中节点 p 的高度定义如下:
- 如果 p 是一个叶子节点,那么它的高度为0.
- 否则,P 的高度是它孩子节点中的最大高度加1。
Ps:可以发现,在该书中,对于高度和深度的定义完全相反,深度是自上而下看,而高度是自下而上看。

表示方法
双Q表示法
(莫名奇妙的感觉这个表示方法在骂人一样)
通过数组进行存储,每个元素有2个域,一个是数值域,另一个则是用于存储其父节点的下标,根节点的父节点下标可考虑用 -1 进行表示。
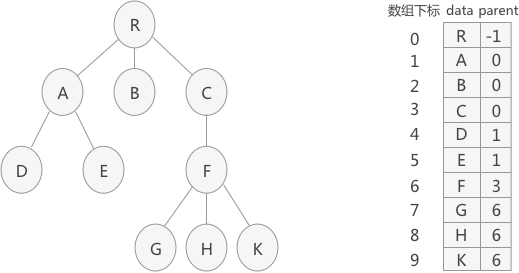
孩子表示法
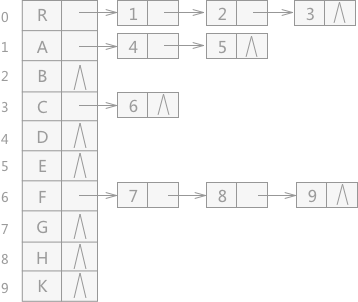
所谓的孩子表示法,即首先用线性表将树中的所有节点存储下来,然后用下标来表示孩子,分别链接在每个节点之后。显而易见,这种方法浪费存储空间并且效率偏低。
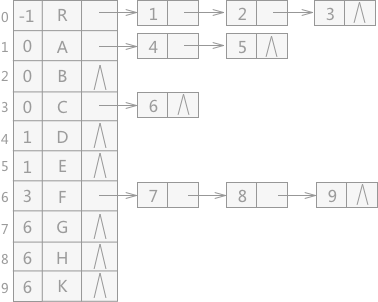
另外,孩子表示法 + 双Q表示法 就诞生出了孩子双Q表示法(??????
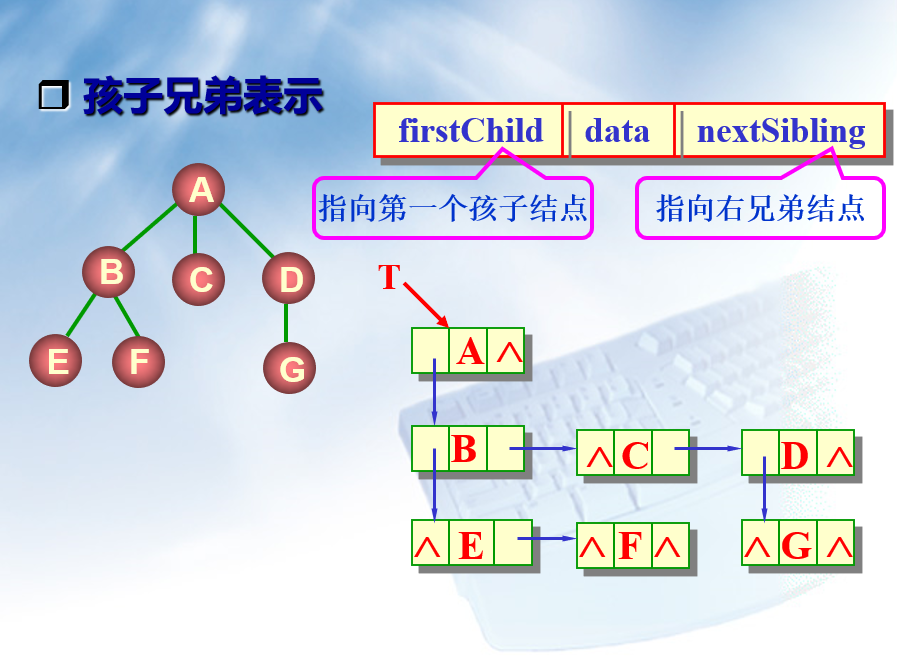
孩子兄弟表示法
在这个方法中,使用链式存储结构来存储普通的树,其每个节点有三个域,分别是孩子指针域,数值域和兄弟指针域。即第一个指针用于将大体自上而下的结构串联起来,数值域用来记录数值,兄弟指针域将树从左至右串联起来。
树和森林的遍历
(此处的遍历算法要和下处的二叉树遍历算法相互区分,避免混淆。但大致思路相同)
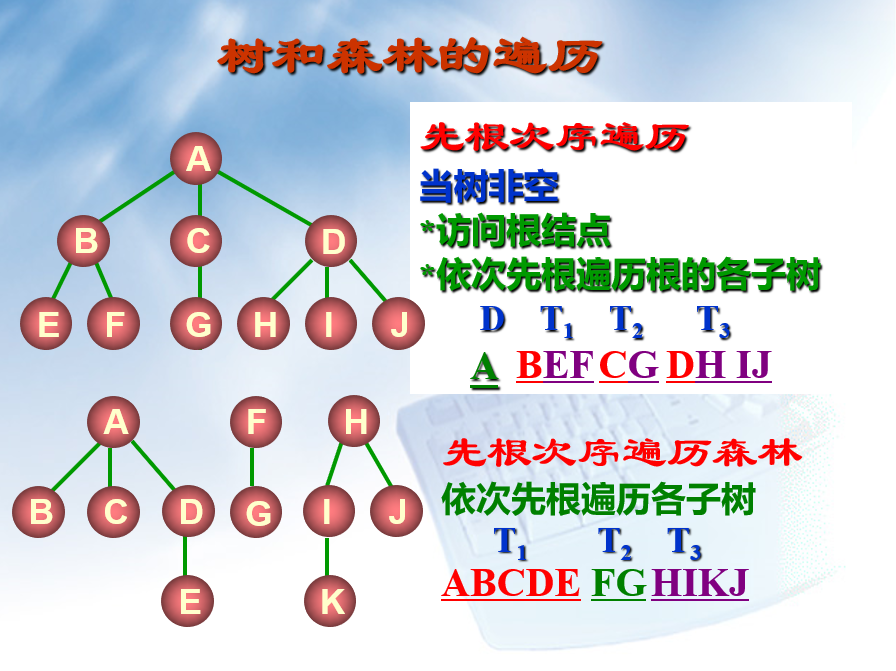
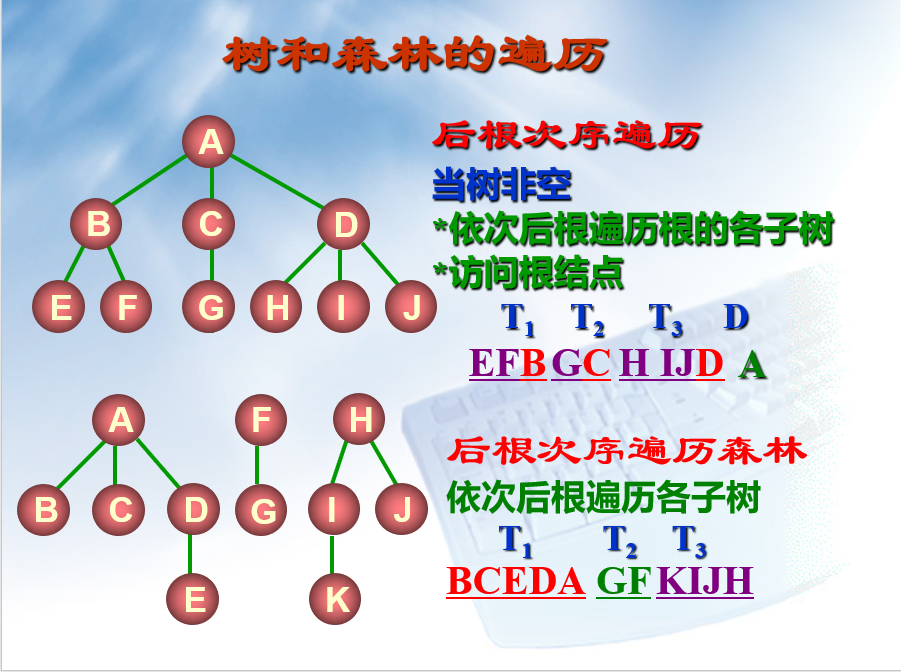
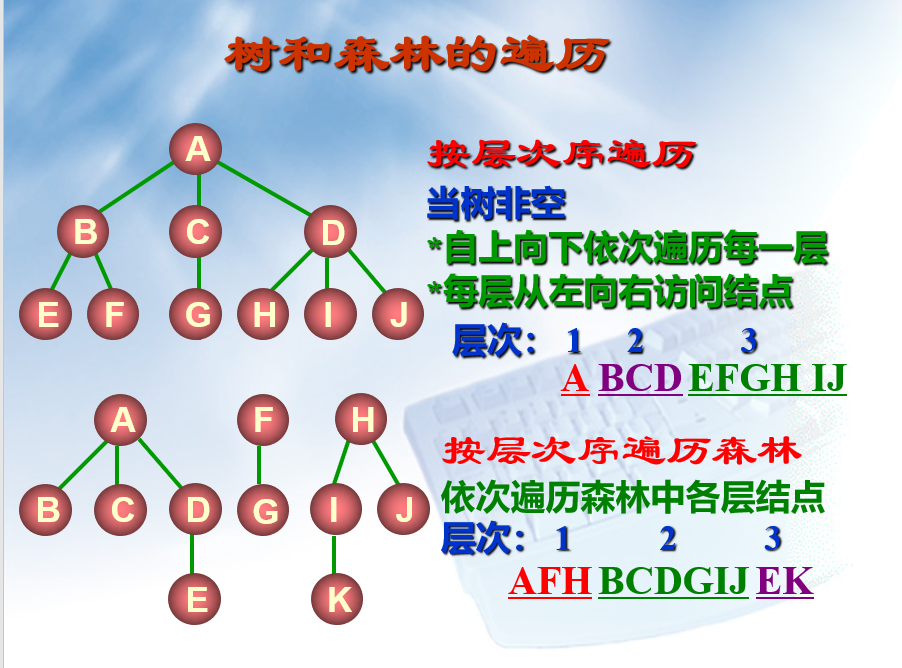
二叉树
定义
二叉树是具有一下属性的有序树:
- 每个节点最多有两个孩子节点。
- 每个孩子节点被命名为左孩子或右孩子。
- 对于每个节点的孩子节点,在顺序上,左孩子先于有孩子。
特性
- 一颗二叉树若有 n 个元素且 n > 0 ,则它一共有 n - 1 条边。(画个图则很容易理解)
- 一颗二叉树的高度若为 h ,则它最少有 h 个元素,最多有 $2 ^ h - 1$个元素。(每一级最少1个元素,则元素个数最少为 h ,每个元素最多2个子节点,则第 i 层的节点个数最多为 $2 ^i - 1$个,元素总数最多为:$\sum_{i = 1}^{h}2^i - 1 = 2 ^h - 1$ 。)
-
一颗二叉树若有 n 个元素,则它的高度最大为 n,最小高度为 $log_2(n+ 1)$。
- 设 T 为非空二叉树,n、$n_E$、$n_I$ 和 h 分别表示 T的节点数,外部节点数,内部节点数和高度,则 T 具有如下性质:
- $h + 1 <= n <=2 ^ {h + 1} - 1$
- $1 <= n_E <= 2 ^h$
- $h <= n_I <= 2 ^h - 1$
- $log(n+1) - 1 <= h <= n - 1$
数组表示
若要通过数组来对二叉树 T 进行表示,需要提前对 T 的位置进行编号。对于 T 的每个位置 p,设f(p) 为整数且定义如下:
- 若 p 是 T 的根节点,则 f(p) = 0;
- 若 p 是 q 的左孩子,则f(p) = 2f(q) + 1;
- 若 p 是 q 的有孩子,则 f(p) = 2f(q) + 2。
通常会采用层编号来对二叉树进行编号,即自上而下,自左至右,从1开始。(0
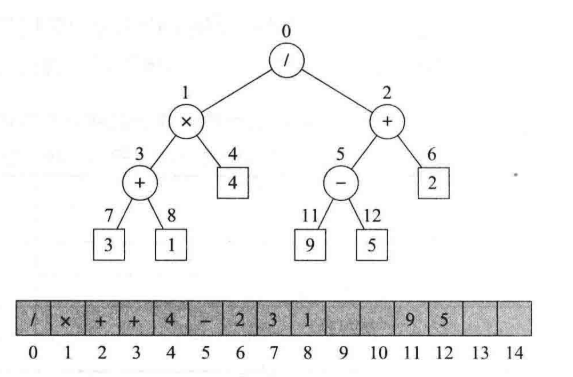
基于数组表示的空间使用情况会极大程度上依赖于树的形状,对于一般的二叉树而言,这种表示方式的指数级的空间要求通常是不被允许的。
链表表示
当使用链表来表示二叉树时,由于二叉树中孩子节点具有先后顺序,因此 children 指针需要区分 left 和 right 片段,而对于一般树,一个节点所拥有的孩子节点之间没有优先级限制。
因此链表中的节点可以拥有 3个域:即:左孩子指针,右孩子指针和数值域。
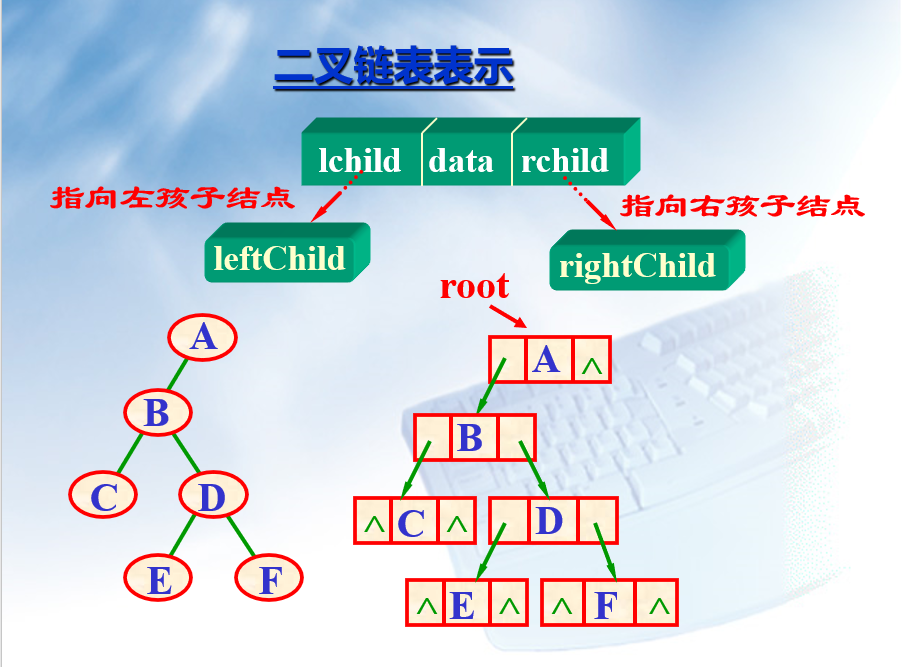
也可以拥有4个域(全看个人设置),即:左孩子指针,右孩子指针, parent 指针和数值域。
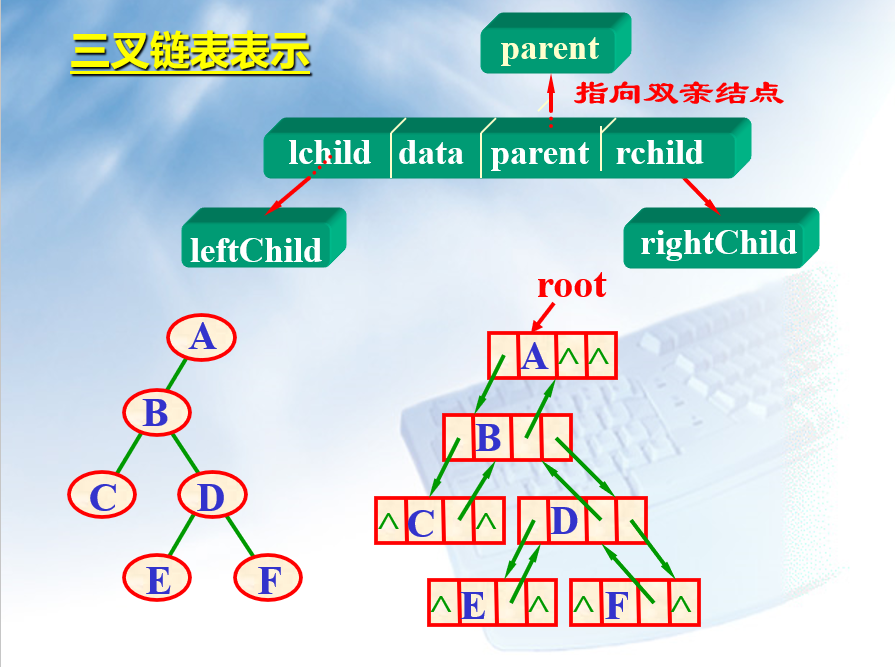
遍历方式
有4种遍历二叉树的常用方法:
- 前序遍历;
- 中序遍历;
- 后序遍历;
- 层次遍历。
前序遍历
若二叉树 T 非空,则:
- 访问根节点(D)
- 前序遍历左子树(L)
- 前序遍历右子树(R)

中序遍历
若二叉树非空,则:
- 中序遍历左子树(L)
- 访问根节点 (D)
- 中序遍历右子树(R)

后序遍历
若二叉树非空,则:
- 后续遍历左子树(L)
- 后续遍历右子树(R)
- 访问根节点(D)

层次遍历

哈夫曼树
哈夫曼树是一类带权路径最短的树,这种树在信息检索中很有用。如用在通讯以及数据传送中构造传输效率最高的二进制编码(哈夫曼编码),也可以用于构造平均执行时间最短的判断过程。
哈夫曼树具有一个特点:即权值越大的节点离根越近,这是因为在计算 WEP 时,其值不仅与权值大小有关,也与到该节点的路径长度有关系。因此将权值越大的节点越靠向根节点可以有效地降低 WEP 数值。 \(WEP = \sum_{i=1}^{n}L(i)*F(i)\) WEP是二叉树的加权外部路径长度(weighted external path length)。
构造过程
首先建立一组二叉树集合,然后从集合中不断选取两个权值最小的二叉树,并且把他们合并成一颗新的二叉树,父节点的值是两颗子树的权值之和,不停重复上述操作,直至选取完集合中所有的点为止。
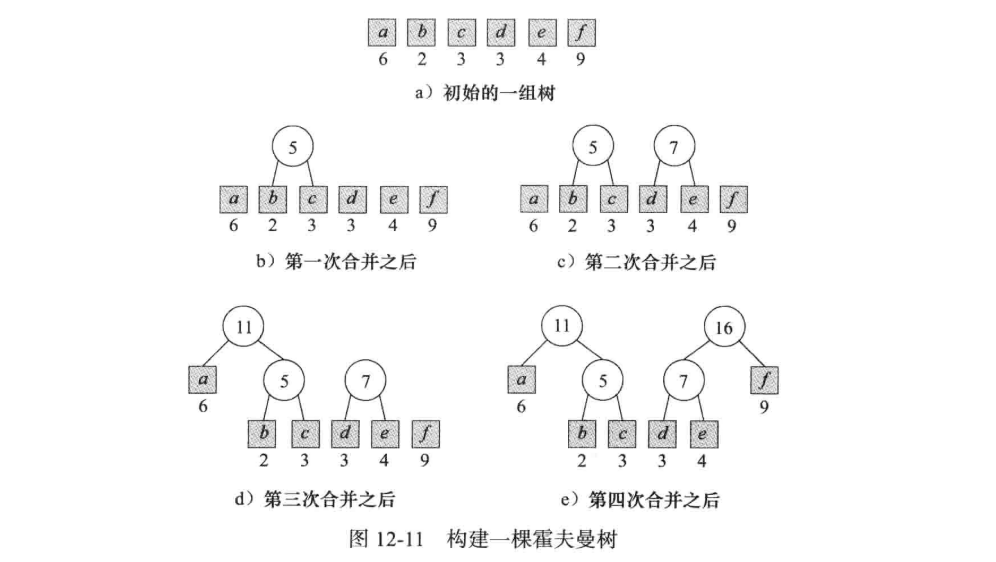

虽然内容不太相关,不过我们也介绍一下哈夫曼编码。
哈夫曼编码
哈夫曼编码是一种文本压缩算法,这种算法依据的是不同符号再一段文本中相对出现的频率。对于一个由字符 a、u、x、z 组成的字符串,长度为1000,若每个字符用 1 个字节来存储,共需要1000个字节,而我们对每个字符用2位二进制来编码(00 = a, 01, 10, 11)那么用2000位空间即可以表示1000 个字符。
当字符出现的频率具有较大的差别时,我们可以通过改变编码长度来缩短整体编码串的长度。毋庸置疑,我们倾向于将出现频率较高的字符编码设置为较短的编码,出现频率较低的字符编码较长。在此处设置编码的时候需要注意,不能设置可能会引起歧义的编码对,不然会对后序进行解码过程造成较大的困难。
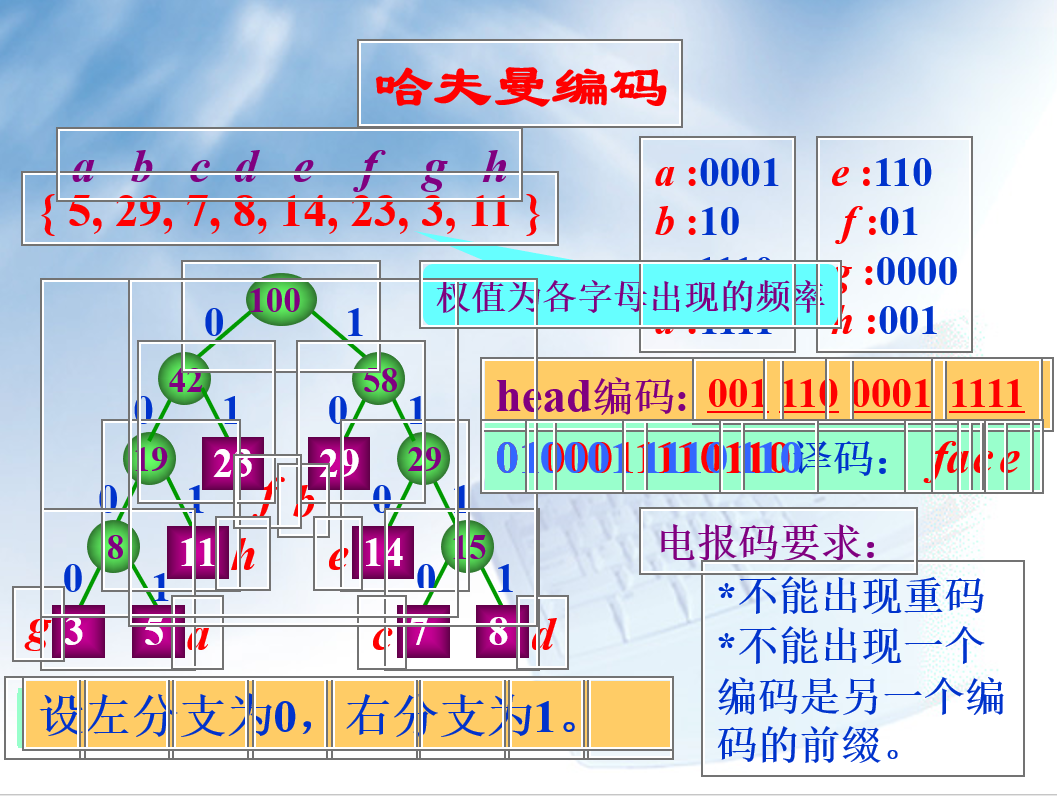
完全二叉树
定义
对于高度为 h 的满二叉树的元素,从第一层到最后一层,每一层中从左到右顺序编号,从 1 到 $2 ^ h - 1$ 。假设从满二叉树中删除 k 个编号为 $2^h - i$ 的元素,其中,$1 <= i <= k < 2 ^h$,所得到的二叉树则被称为完全二叉树。
是不是不太能够理解?看看下面这个定义。
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
对于满二叉树的定义来说,国内教材和国外教材的定义方面存在一定的差异。下面分别给出:
国内定义:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。 也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。 国外定义:满二叉树的结点要么是叶子结点,度为0,要么是度为2的结点,不存在度为1的结点。
性质
- 在完全二叉树中,一个元素与其孩子的编号有非常好的对应关系,设完全二叉树的一个元素编号为 i ,其中 $1 <= i <= n $,有如下关系成立:
- 如果 i = 1,则该元素为二叉树的根。若 i > 1,则其父节点的编号为 $[i / 2]$。
- 如果 2i > n,则该孩子没有左孩子。否则,其左孩子的编号为2i。
- 如果2i + 1 > n,则该孩子没有右孩子。否则,其孩子的编号为 2i + 1。
- 设 T 为完全二叉树,n、$n_E$、$n_I$ 和 h 分别表示 T的节点数,外部节点数,内部节点数和高度,则 T 具有如下性质:
- $2h + 1 <= n <=2 ^ {h + 1} - 1$
- $h + 1 <= n_E <= 2 ^h$
- $h <= n_I <= 2 ^h - 1$
- $log(n+1) - 1 <= h <= (n - 1)/2$
- 在非空完全二叉树 T 中,有 $n_E$ 个外部节点和 $n_I$ 个内部节点,则有$n_E = n_I + 1$。
二叉查找树
二叉查找树,顾名思义,其是二叉树且大部分情况下用于查找。其具有如下的属性:
- 每个节点左边的元素的数值均小于该节点的数值
- 每个节点右边的数值均大于该节点的数值。
(和 sorted array 大概相同)
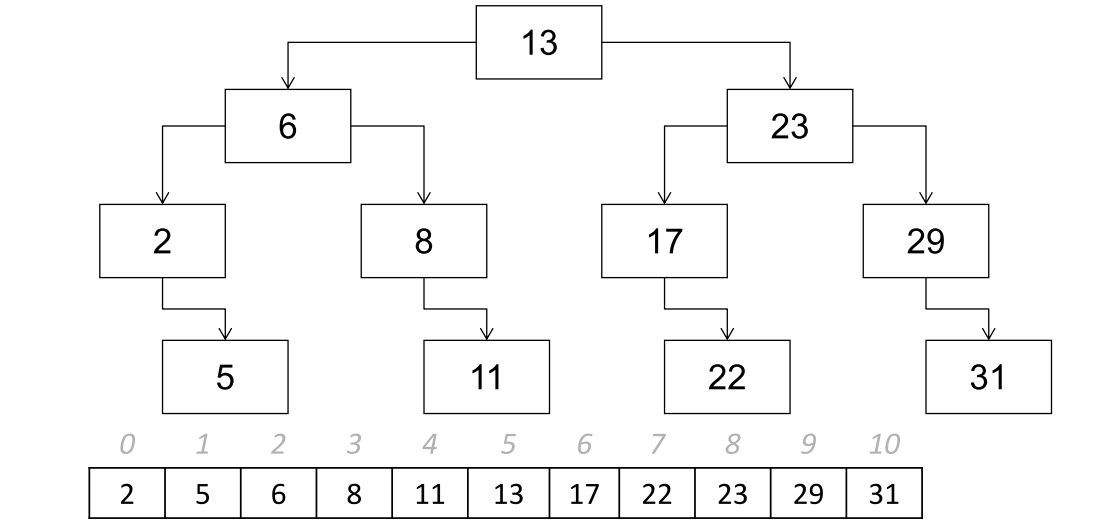
搜索过程:
假设搜索的值为vals,首先与根进行比较,若 vals < 13 ,则向左(下一步和6比较),若 vals > 13 ,则向右(下一步和23比较),如此进行迭代的操作,直至找到值为 vals 的节点或无值可以再进行比较,则整个搜索过程结束。
线索二叉树
线索二叉树大致与二叉树相同,不同的是,线索二叉树遵循某种遍历(前序、中序、后序),当某个节点没有左孩子时,则该节点的左孩子指针指向遍历中的前驱(简单来说就是在遍历序列中排在前前面一个位置的节点),若某个节点没有有孩子时,则该节点的有孩子指针指向遍历中的后继(遍历序列中排在该节点后面一个位置的节点)。
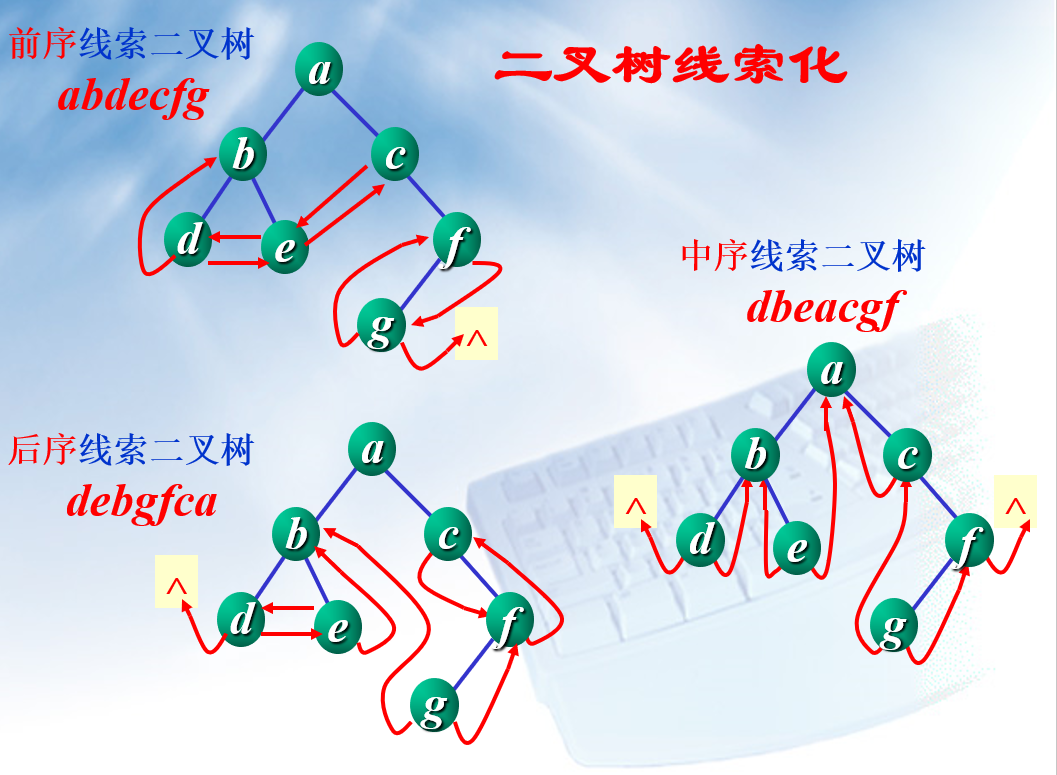
仅仅从理解上来看的话,比较简单,只需要在其无左孩子/有孩子时,根据对应的遍历序列,将线索链接起来。
在设置数据结构时,由于不太清楚其左孩子/右孩子指针所指向的究竟时孩子节点还是遍历顺序的节点,因此分别需要两个 tag 来对指针进行标记,0 代表指向孩子节点, 1 指向序列中的节点(不过具体设置依个人而定,此处仅仅提供一个思路)。

森林
(待补充
森林和树之间的相互转换
(看图就完事了
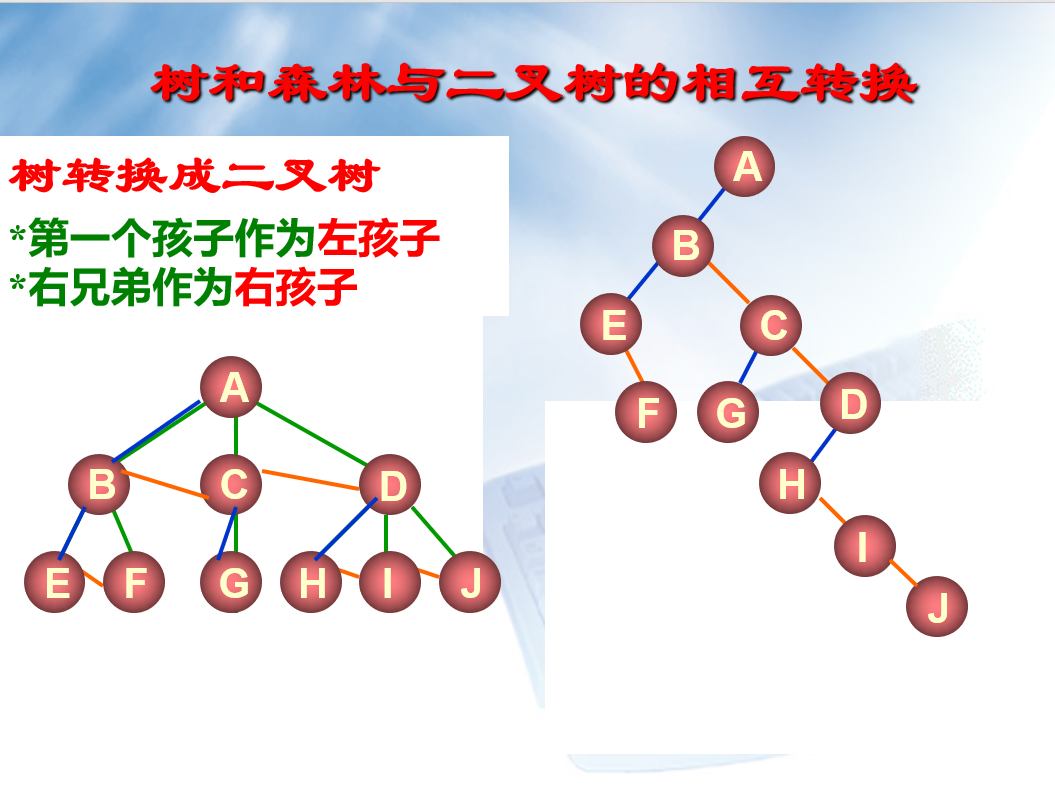
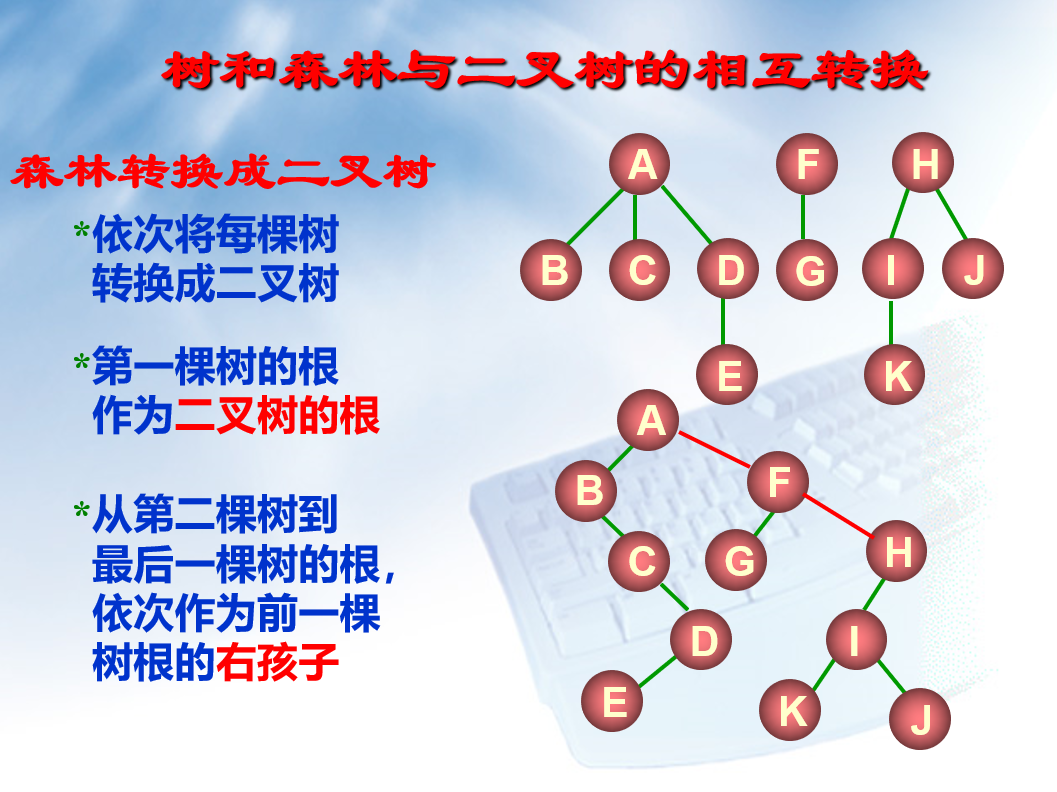
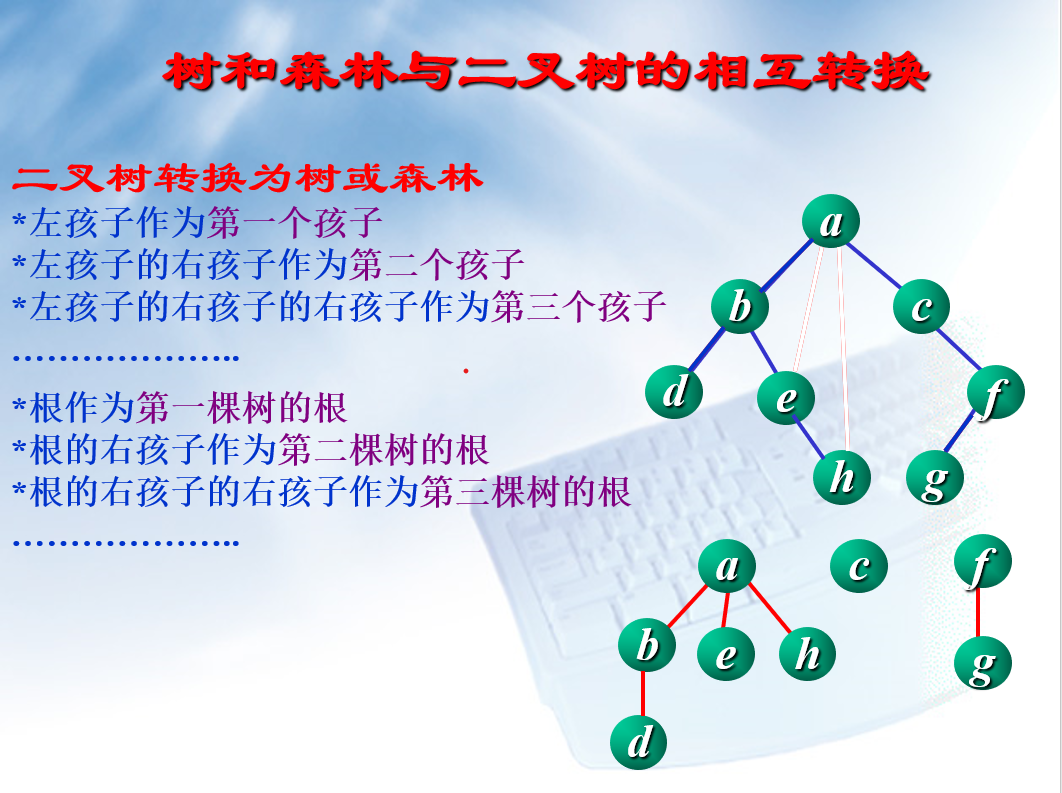
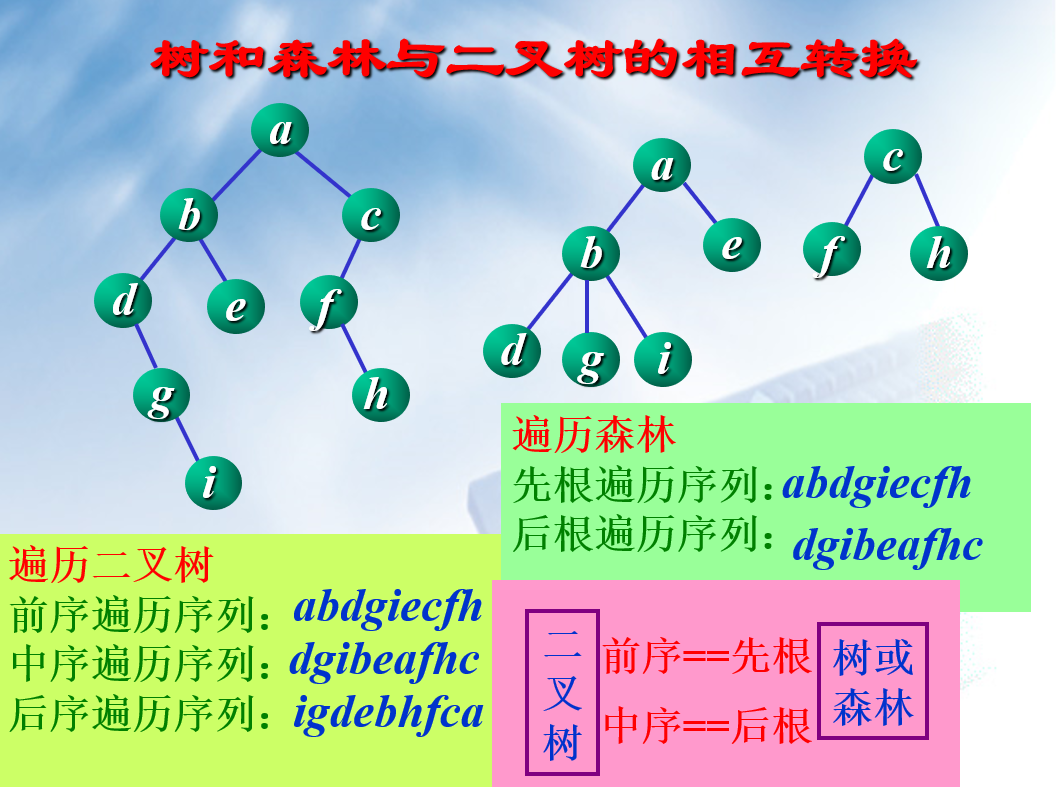
字典树
(待补充
红黑树
(待补充
