07 Apr 2022 2286字 8分

队列

队列是一种特殊线性表，与栈相同。队列的插入和删除操作分别在两端进行，与栈不相同，因此队列是一个先进先出的线性表。

定义

队列是一个线性表，其插入和删除操作分别在表的不同端进行。插入元素的那一端称为队尾（back 或 rear），删除元素的那一端称为队首（front）。

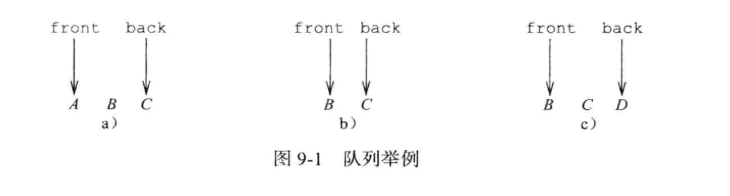
记忆队列时，可以联想我们平时排队的情形。在排队的过程中遵守先来先到原则，也即是先进先出原则。

抽象数据类型（ADT）

在队列当中，常见的操作有如下：

functions	runtimes	description
q.dequeue()	O(1)	removes front value and returns it;throws error if queue is empty
q.enqueue(value)	O(1)	places given value at back of queue
q.isEmpty()	O(1)	returns true of queue has no elements
q.peek()	O(1)	returns front value without removing;throws an error if queue is empty
q.size()	O(1)	return number of elements in queue

数组实现

若要通过数组来实现队列，首先需要考虑将哪端作为队首，哪端作为队尾。

假如将 index = 0 作为队首，即 location(i) = i;

队列的第 i 个元素存储在 queue[i] 中，queueFront = 0，队列长度 = queueBack + 1，在队列空时,queueBack = -1。

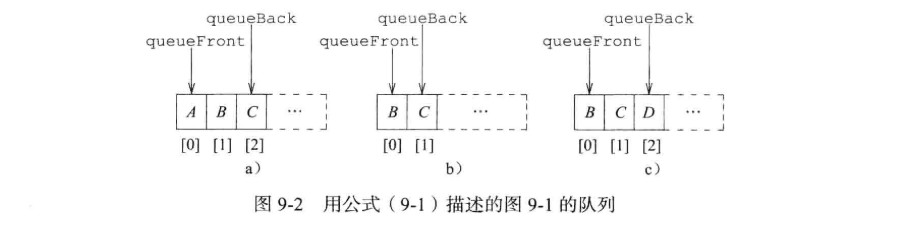
当进行插入操作时，所需要的时间 Θ(1)（queueBack 加1，再把元素插入到 queue[queueBack]当中），当进行删除操作时，所需要的时间是 Θ(n)，其中 n 为删除之后剩余元素的个数。

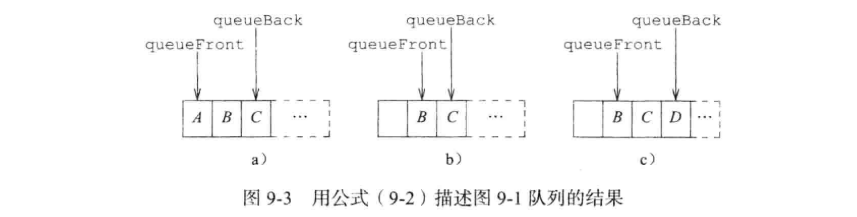
假如队首位置不固定时，即 location(i) = location(队首元素) + i

此时，删除操作所需要的时间将减少至 Θ（1）。

然而，当这样使用数组时，可能会出现许多未使用空间，且数组长度已经被扩大数倍。这个时候我们可以将数组视为一个环（将数组视为环是为了理解，其实是对下标进行设置），就可以利用这些空余空间，同时插入和删除的最坏时间复杂度都会变成 Θ（1) ，

这也被称为循环队列。

循环队列

对于循环队列，也有两种实现方式：

当然，无论以何种方式进行实现，队列元素的个数最多是 $arrayLength - 1$ 。

void Initqueue (SqQueue *&q) 
{  
   q=(SqQueue *)malloc(sizeof(SqQueue));
   q->rear = q->front = 0;
}

bool QueueEmpty (SqQueue *q ) 
{
    if ( q->rear == q->front)  return true;
    else	return false;
}
bool enQueue (SqQueue *&q, elemtype e ) 
{
    if ( q->front= =(q->rear+1)% maxsize )
          return false;
    q->rear = ( q->rear+1) % maxsize;
    q->data[q->rear] = e;
    return true;
}
bool deQueue (SqQueue *q; elemtype &e ) 
{
    if ( q->front==q->rear)
          return false;		
    q->front = ( q->front+1) % maxsize;
    e = q->data[q->front];
    return true;
}

链表实现

同理，在使用链表对队列进行实现过程中，需要考虑头的位置。在链表中，则是考虑指针的方向。1. 指针由头指向尾，2. 指针由尾指向头。

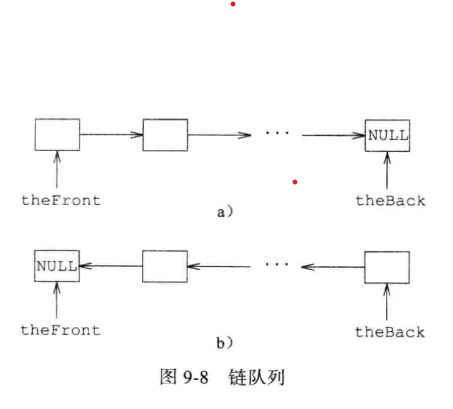
对于这两种方式，插入操作均没有差别，而对于删除操作，第一种方式会更加方便，因此我们通常采用从头至尾的链接方向。

操作如下：（贴图就对了）

优先队列

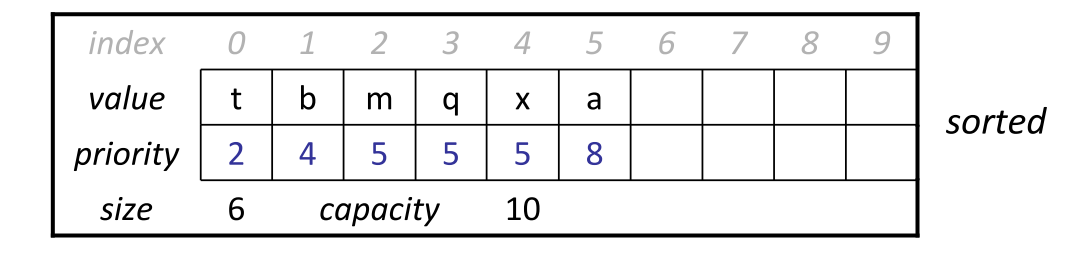
优先队列是一种特殊的队列，在优先队列中，其中的元素被赋予了不同的权值大小，代表了各个元素的优先级。

可能会存在的操作如下：

actions	description
pq.enqueue(value, pri)	adds value to queue,with the given priority number
pq.dequeue()	return the value in the queue with most urgent(minimum)priority;thros an error if empty
pq.peekPriority()	returns priority of most urgent priority element;throws error if queue is empty
pq.isEmpty()	return true if queue contains no elements(size 0)
pq.size()	returns the number of elements in the queue
out « pq	return / print a string such as “{3, 42, -7, 15}”
pq.changePriority(value, pri)	alters an existing element’s priority to be more urgent
pq.clear()	removes all elements of the queue
pq.peek()	returns most urgent priority element without removing it;throws error if queue is empty

实际应用

（暂略。累了去休息了

队列-知识点

队列

定义