栈
栈和队列是应用频率非常高的数据结构。对于栈,其有数组实现方式,也有链表的实现方式。故把握其数据特性十分重要。
定义
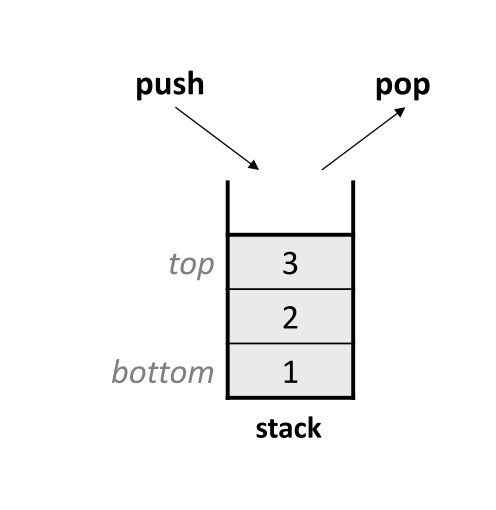
栈(stack)是一种特殊的线性表,其插入(入栈)和删除(出栈)都是在表的同一端进行。这一段也被称为栈顶(top),另一端被称为栈底(bottom)。栈是一个先进后出(last-in-first-out,LIFO)的数据结构
抽象数据类型(ADT)
对于栈,主要的操作有如下几个:
| functions | description |
|---|---|
| push(value) | add an element to the top of the stack. |
| pop() | aremove and return the top element in the stack. |
| peak() | return(but do not remove)the top element in the stack. |
接下来看看《数据结构、算法与应用 c++ 描述中》所给出的ADT定义:


数组实现
用数组来实现栈并不是一个难事,只需要把握住栈的特性:先进后出,即可。具体的实现看下面图片即可:(写的很好)


ps:在上述代码中,允许指定初始容量十分重要,在一定程度上可以避免后续操作对数组大小进行改变。
链表实现
当通过链表实现栈时,必须确定用链表的哪一端来代表栈顶。其实对于这个问题,已经有明确的答案。若选择右端作为栈顶,则栈操作 top、push 和 pop 的实现的时间复杂度为 O(size)。若选择左端作为栈顶,则栈操作top、push 和 pop 的实现的时间复杂度为 Θ(1)。因此我们选择链表的左端作为栈顶。

栈的应用
栈的实现虽然不困难,但由于其具有先进后出的特性,因此也适合来解决类似于此种特性的问题,就如同递归函数栈一般。根据个人理解是栈具有存储以往信息并返回的功能,因此在部分需要进行试错的问题(如迷宫)可以使用。同时,左括号,右括号的匹配也神似入栈、出栈的过程,因此也可以用于括号匹配当中。
括号匹配
此处仅仅考虑的是单括号匹配的问题,因此实现过程较简单。

汉诺塔问题
对于汉诺塔问题,既可以采用递归解决,也可以采用栈解决。
递归解决
首先讲讲递归的思路:
你有 N 个盘子,3 座塔, N 的盘子从大到小,自下往上的堆叠在塔1的位置(下述通过Ⅰ来描述),我们需要做的,就是把Ⅰ的盘子,按照原有的顺序堆叠在Ⅱ。对于递归的问题,往往我们需要想清楚其基本情况和 base case 。当 N = 2时,我们需要把Ⅰ处最上方的盘子移至 Ⅲ,然后将最重的盘子移至Ⅱ,再把Ⅲ的盘子移至Ⅱ。当N = 3时,我们把Ⅰ最上方两个盘子移至Ⅲ(牢记,一次只能移动一个),然后将最重的盘子移至Ⅱ处。对于N时,我们需要把Ⅰ上方 N - 1 个盘子移至 Ⅲ 处,然后把最大的盘子移到Ⅱ,最后再将Ⅲ的 N - 1 个盘子移至 Ⅱ。Obviously,这里就出现了重复情况,而递归就是将一个问题通过重复不断的情况进行循环,直至基本情况,然后不断返回结果,最后得出解。

另外,当最终的盘子移动至Ⅱ时,则不需要再管他,因为他已经是目前最重的盘子,后续步骤也同理。
时间复杂度:$Θ(2^n)$。
栈解决
思路大致与递归时相同,区别在于,通过栈实现时,对数据的存取需要自己手动实现。

列车车厢重排
略。
离线等价类问题
略。(或待补充
迷宫问题
迷宫问题具体的题目要求不要过多赘述,下述主要提供一下思路。
迷宫的问题大致分为两类:一是找到能够到达的路径,二是找到最短的路径。这两者的区别在于后者是小于等于1的,即存在一条最短的路径或无路径可以到达出口。
在解决问题的过程中,可以将迷宫的位置考虑为状态,即存在可走和不可走的状态,同时,也存在走过和未走过的状态。前者是为了找到到达出口的路径,后者则是为了避免重复走相同的路径而陷入死循环中。同时也方向也存在4个状态,即上下左右。


