基于 pytorch 实现数字的识别

实验内容

基于 pytorch 实现数字的识别。

ps:此文章的代码COPY自网上。

实验原理

要想用 pytorch 实现数字的识别，有许多东西需要给大家讲讲的。

首先要和大家讲讲神经网络

神经网络（ANN）

定义

​ 人工神经网络（英语：Artificial Neural Network，ANN），简称神经网络（Neural Network，NN）或类神经网络，在机器学习和认知科学领域，是一种模仿生物神经网络（动物的中枢神经系统，特别是大脑）的结构和功能的数学模型或计算模型，用于对函数进行估计或近似。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统，通俗地讲就是具备学习功能。现代神经网络是一种非线性统计性数据建模工具，神经网络通常是通过一个基于数学统计学类型的学习方法（Learning Method）得以优化，所以也是数学统计学方法的一种实际应用，通过统计学的标准数学方法我们能够得到大量的可以用函数来表达的局部结构空间，另一方面在人工智能学的人工感知领域，我们通过数学统计学的应用可以来做人工感知方面的决定问题（也就是说通过统计学的方法，人工神经网络能够类似人一样具有简单的决定能力和简单的判断能力），这种方法比起正式的逻辑学推理演算更具有优势。

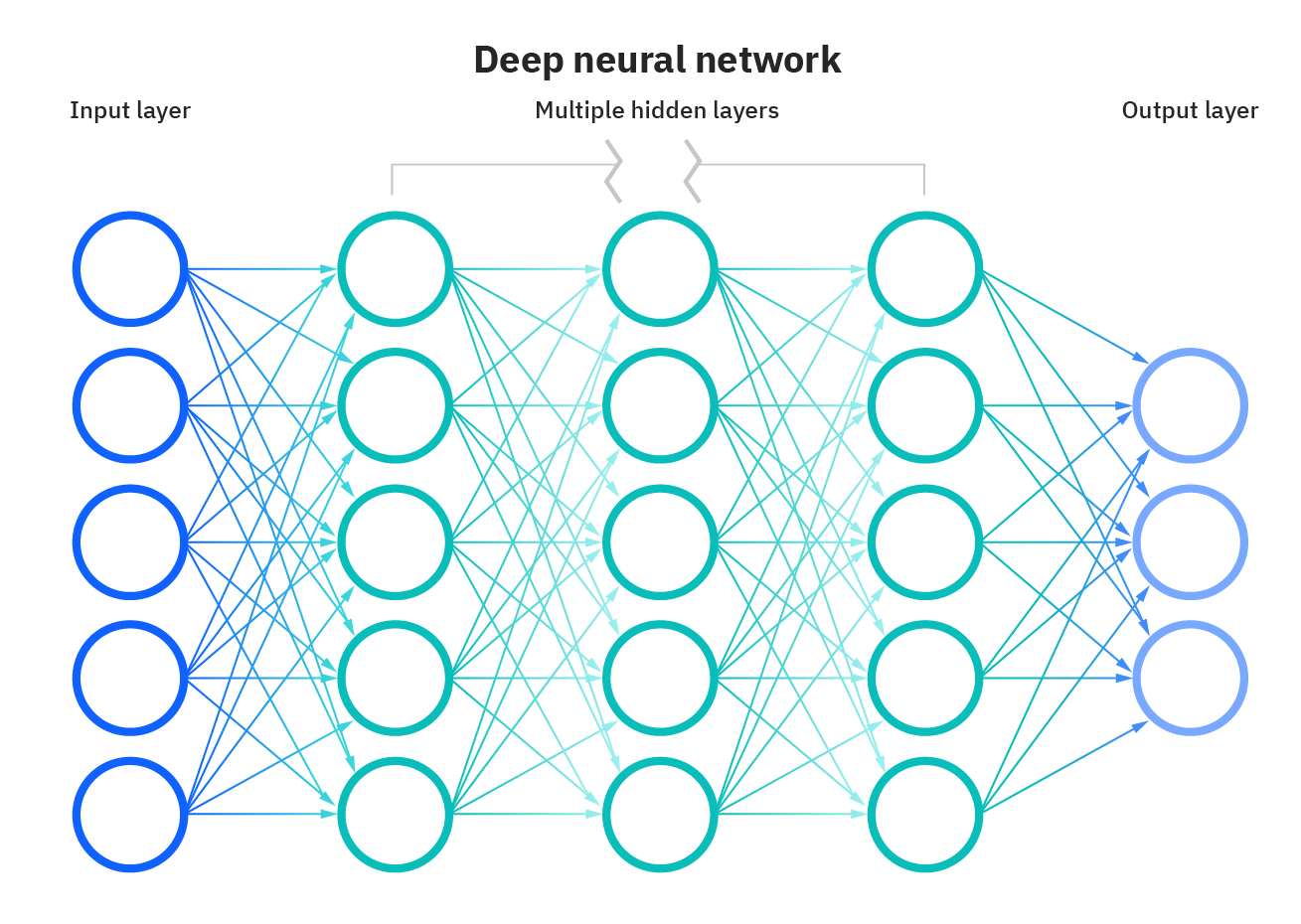
和其他机器学习方法一样，神经网络已经被用于解决各种各样的问题，例如机器视觉和语音识别。这些问题都是很难被传统基于规则的编程所解决的。

神经元

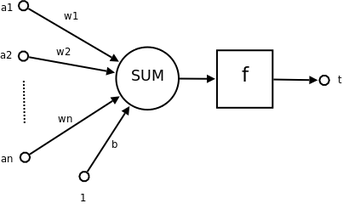
• $a1-an$ 为输入向量的各个分量
• $w1-wn$ 为神经元各个突触的权值
• $b$ 为偏置
• $f$ 为传递函数，通常为非线性函数。一般有$traingd(),tansig(),hardlim()$。
• t为神经元输出

数学表示

• 为权向量，为的转置
• 为输入向量
• 为偏置
• 为传递函数

可见，一个神经元的功能是求得输入向量与权向量的内积后，经一个非线性传递函数得到一个标量结果。

单个神经元的作用：把一个n维向量空间用一个超平面分割成两部分（称之为判断边界），给定一个输入向量，神经元可以判断出这个向量位于超平面的哪一边。

输入层（Input layer)

​ 众多神经元（Neuron）接受大量非线形输入消息。输入的消息称为输入向量。

隐藏层(Hidden layer)

​ 隐藏层， 又称为隐层，是输入层和输出层之间众多神经元和链接组成的各个层面。隐层可以有一层或多层。隐层的节点（神经元）数目不定，但数目越多神经网络的非线性越显著，从而神经网络的强健性（控制系统在一定结构、大小等的参数摄动下，维持某些性能的特性）更显著。习惯上会选输入节点1.2至1.5倍的节点。

输出层（Output layer)

​ 消息在神经元链接中传输、分析、权衡，形成输出结果。输出的消息称为输出向量。

激活层

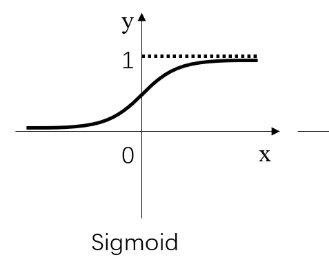
​ 简而言之，激活层是为矩阵运算的结果添加非线性的。常用的激活函数有三种，分别是阶跃函数、Sigmoid和ReLU。不要被奇怪的函数名吓到，其实它们的形式都很简单，如下图：

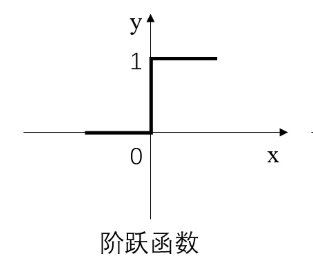
​ 阶跃函数：当输入小于等于0时，输出0；当输入大于0时，输出1。

​ Sigmoid：当输入趋近于正无穷/负无穷时，输出无限接近于1/0。

​ ReLU：当输入小于0时，输出0；当输入大于0时，输出等于输入。

如何运作

将各个节点想象成其自身的线性回归模型，由输入数据、权重、偏差（或阈值）和输出组成。公式大概是这样的：

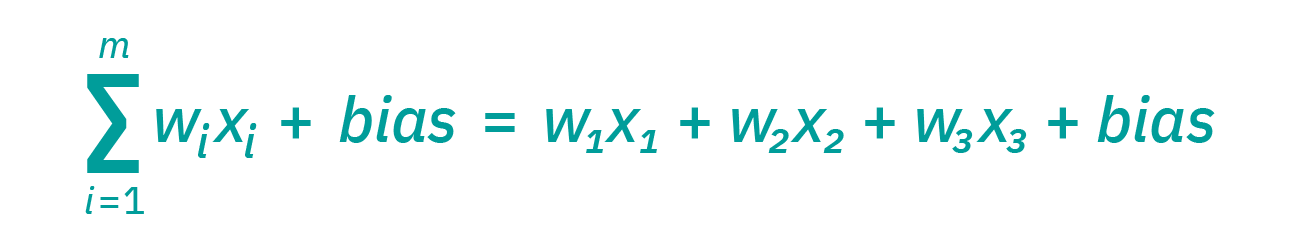
一旦确定了输入层，就会分配权重。 这些权重有助于确定任何给定变量的重要性，与其他输入相比，较大的权重对输出的贡献更大。 将所有输入乘以其各自的权重，然后求和。 之后，输出通过一个激活函数传递，该函数决定了输出结果。 如果该输出超出给定阈值，那么它将“触发”（或激活）节点，将数据传递到网络中的下一层。 这会导致一个节点的输出变成下一个节点的输入。 这种将数据从一层传递到下一层的过程规定了该神经网络为前馈网络。

随着我们开始思考更实际的神经网络用例，例如图像识别或分类，我们将利用监督式学习或标签化数据集来训练算法。 当我们训练模型时，我们将使用成本（或损失）函数来评估其准确性。 这通常也称为均方误差 (MSE)。 在下面的等式中，

• $i$ 表示样本的索引，
• $y-hat$ 是预测的结果，
• $y$ 是实际值，而 $m$ 是样本的数量。

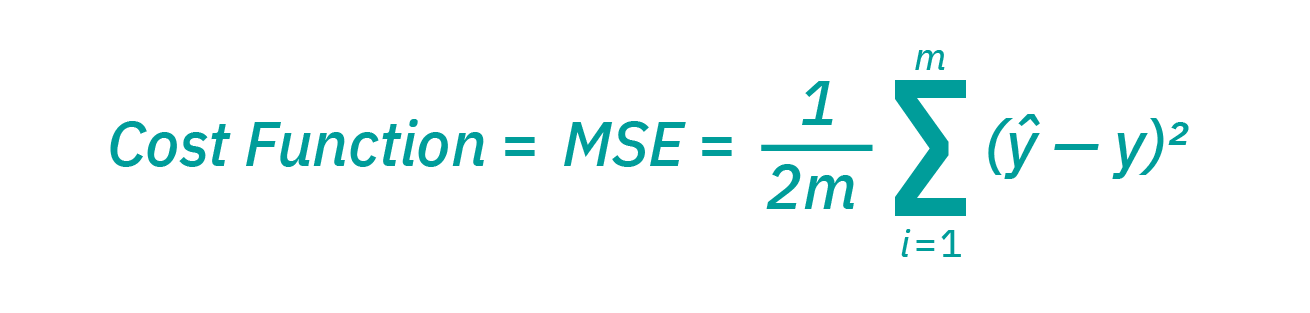
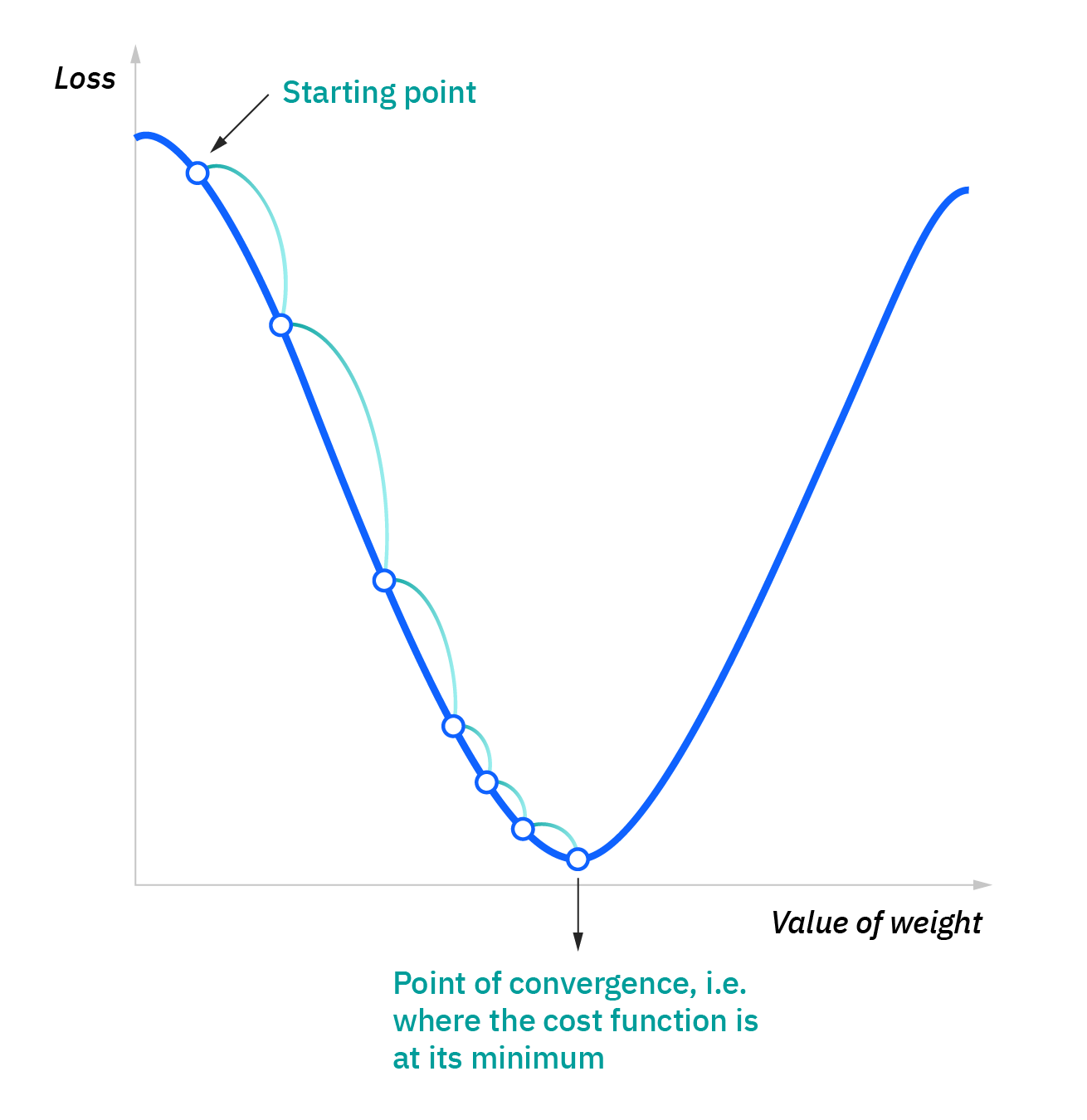
最终的目标是，使我们的成本函数最小化，以确保对任何给定观测的拟合的正确性。 当模型调整其权重和偏差时，它使用成本函数和强化学习来达到收敛点或局部最小值。 算法通过梯度下降调整权重，这使模型可以确定减少错误（或使成本函数最小化）的方向。 通过每个训练示例，模型的参数不断调整，逐渐收敛到最小值。

种类

​ 依学习策略分类主要有：

• ​ 监督式学习网络；
• ​ 无监督式学习网络；
• ​ 混合式学习网络；
• ​ 联想式学习网络；
• ​ 最适化学习网络。

​ 依网络架构分类主要有：

• ​ 前馈神经网络；
• ​ 循环神经网络；
• ​ 强化式架构。

（说了这么多，其实你记不住也完全没有关系的）

神经网络与深度学习

​ 当将深度学习应用在神经网络上时，一个很简单的思想即是将神经网络的层数加多。

​ 其实呢， 深度学习是为了让层数较多的多层神经网络可以训练，能够work而演化出来的一系列的 新的结构和新的方法。

​ 新的网络结构中应用最广泛的的就是CNN，大量应用在计算机视觉领域，它解决了传统较深的网络参数太多，很难训练的问题，使用了“局部感受野”和“权植共享”的概念，大大减少了网络参数的数量。一些研究表明，这种对信息的层次化抽取与提练很符合视觉类任务在人脑上的工作原理。CNN这个方向上结构经过几年的发展，出来了很多的经典网络结构，如VGG、Inception、ResNet等。除了CNN之外，在序列数据的处理上，RNN被广泛应用，RNN方向上也有很多创新的网络结构被提出，比如LSTM。

​ 如果你不知道CNN 的话， 暂时也不用着急噢！（下面会给你讲的

深度神经网络（DNN）

​ 神经网络是基于感知机的扩展，而DNN可以理解为有很多隐藏层的神经网络。多层神经网络和深度神经网络DNN其实也是指的一个东西，DNN有时也叫做多层感知机。

​ 　从DNN按不同层的位置划分，DNN内部的神经网络层可以分为三类，输入层，隐藏层和输出层,如下图示例，一般来说第一层是输入层，最后一层是输出层，而中间的层数都是隐藏层。

​

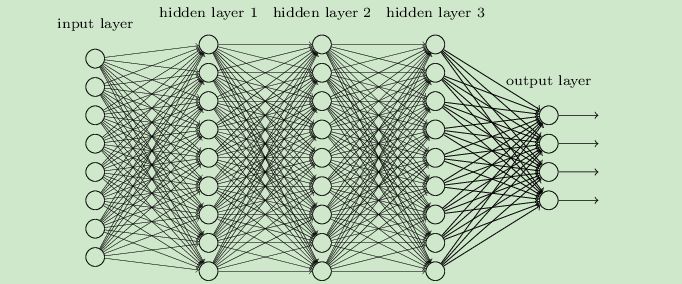
层与层之间是全连接的，也就是说，第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。虽然DNN看起来很复杂，但是从小的局部模型来说，还是和感知机一样，即一个线性关系：$Z = \sum{w_ix_i + b}$ 加上一个激活函数 $α(z)$。

向前传播算法

向后传播算法

​ 由于只是简单的和大家提一下深度神经网络，因此上面两个方面的话就不细提了，感兴趣的话建议自己查询哦。（不是

卷积神经网络(CNN)

卷积操作是什么

​ 首先，多层感知机的输入是二维图像 $X$，其隐藏表示 $H$ 在数学上是一个矩阵，在代码中表示为二维张量。 其中 $X$ 和 $H$ 具有相同的形状。 为了方便理解，我们可以认为，无论是输入还是隐藏表示都拥有空间结构。

​ 使用 $[X]i,_j[X]_i,_j$ 和 $[H]_i,_j[H]_i,_j$ 分别表示输入图像和隐藏表示中位置$(i, j)$ 处的像素。 为了使每个隐藏神经元都能接收到每个输入像素的信息，我们将参数从权重矩阵（如同我们先前在多层感知机中所做的那样）替换为四阶权重张量 $W$。假设 $U$ 包含偏置参数，我们可以将全连接层形式化地表示为 \([H]_{i, j} = [U]_{i, j} + \sum_k\sum_l[W]_{i, j, k, l}[X]_{k, l} = [U]_{i, j} + \sum_k\sum_l[V]_{i, j, a, b}[X]_{i + a, j + b}\) ​ 其中，从 $W$ 到 $V$ 的转换只是形式上的转换，因为在这两个四阶张量的元素之间存在一一对应的关系。 我们只需重新索引下标 $(k,l)$，使 $k=i+a、l=j+b$， 由此可得 $[V]{i,j,a,b}=[W]{i,j,i+a,j+b}$ 。 索引 $a$ 和 $b$ 通过在正偏移和负偏移之间移动覆盖了整个图像。 对于隐藏表示中任意给定位置 $(i, j)$ 处的像素值 $[H]i,j$，可以通过在 $x$ 中以 $(i,j)$ 为中心对像素进行加权求和得到，加权使用的权重为 $[V]{i,j,a,b}$ 。

​ 现在引用上述的第一个原则：平移不变性。 这意味着检测对象在输入 XX 中的平移，应该仅仅导致隐藏表示 $H$ 中的平移。也就是说，$V$ 和 $U$ 实际上不依赖于 $(i,j)$ 的值，即 $[V]{i,j,a,b}=[V]{a,b}$。并且 $U$ 是一个常数，比如 $u$。因此，我们可以简化 $H$ 定义为： \([H]_{i, j} = u + \sum_a\sum_b[V]_{a, b}[X]_{i+a, j+b}\) ​ 这就是 卷积 （convolution）。我们是在使用系数$[V]{a,b}$ 对位置 $(i,j)$ 附近的像素 $(i+a,j+b)$ 进行加权得到$[H]{i,j}$。 注意，$[V]{a,b}$ 的系数比 $[V]{i,j,a,b}$ 少很多，因为前者不再依赖于图像中的位置。这就是显著的进步！

​ 在数学中，两个函数（比如$ f,g:Rd→Rf,g:Rd→R$）之间的“卷积”被定义为 \((f∗g)(x)=∫f(z)g(x−z)dz.(f∗g)(x)=∫f(z)g(x−z)dz.\) 也就是说，卷积是测量 $f$ 和 $g$ 之间（把其中一个函数“翻转”并移位 xx 时）的重叠。 当我们有离散对象时，积分就变成求和。例如：对于由索引为$Z$ 的、平方可和的、无限维向量集合中抽取的向量，我们得到以下定义： \((f∗g)(i)=∑af(a)g(i−a).(f∗g)(i)=∑af(a)g(i−a).\) 对于二维张量，则为 ff 的索引 $(a,b)$ 和 $g$ 的索引 $(i−a,j−b)$ 上的对应和： \((f∗g)(i,j)=∑a∑bf(a,b)g(i−a,j−b).\)

卷积层

​ 卷积层是一组平行的特征图（feature map），它通过在输入图像上滑动不同的卷积核并执行一定的运算而组成。此外，在每一个滑动的位置上，卷积核与输入图像之间会执行一个元素对应乘积并求和的运算以将感受野内的信息投影到特征图中的一个元素。这一滑动的过程可称为步幅$ Z_s$，步幅 $Z_s $是控制输出特征图尺寸的一个因素。卷积核的尺寸要比输入图像小得多，且重叠或平行地作用于输入图像中，一张特征图中的所有元素都是通过一个卷积核计算得出的，也即一张特征图共享了相同的权重和偏置项。

池化层（Pooling layer)

​ 池化（Pooling）是卷积神经网络中另一个重要的概念，它实际上是一种非线性形式的降采样。有多种不同形式的非线性池化函数，而其中“最大池化（Max pooling）”是最为常见的。它是将输入的图像划分为若干个矩形区域，对每个子区域输出最大值。

直觉上，这种机制能够有效地原因在于，一个特征的精确位置远不及它相对于其他特征的粗略位置重要。池化层会不断地减小数据的空间大小，因此参数的数量和计算量也会下降，这在一定程度上也控制了过拟合。通常来说，CNN的网络结构中的卷积层之间都会周期性地插入池化层。池化操作提供了另一种形式的平移不变性。因为卷积核是一种特征发现器，我们通过卷积层可以很容易地发现图像中的各种边缘。但是卷积层发现的特征往往过于精确，我们即使高速连拍拍摄一个物体，照片中的物体的边缘像素位置也不大可能完全一致，通过池化层我们可以降低卷积层对边缘的敏感性。

池化层每次在一个池化窗口（depth slice）上计算输出，然后根据步幅移动池化窗口。下图是目前最常用的池化层，步幅为2，池化窗口为的二维最大池化层。每隔2个元素从图像划分出的区块，然后对每个区块中的4个数取最大值。这将会减少75%的数据量。

​ 除了最大池化之外，池化层也可以使用其他池化函数，例如“平均池化”甚至“L2- 范数“ 池化”等。过去，平均池化的使用曾经较为广泛，但是最近由于最大池化在实践中的表现更好，平均池化已经不太常用。

​ 由于池化层过快地减少了数据的大小，目前文献中的趋势是使用较小的池化滤镜，甚至不再使用池化层。

​ RoI池化(Region of Interest)是最大池化的变体，其中输出大小是固定的，输入矩形是一个参数。

​ 池化层是基于 Fast-RCNN 架构的卷积神经网络的一个重要组成部分。

全连接层

​ 最后，在经过几个卷积和最大池化层之后，神经网络中的高级推理通过完全连接层来完成。就和常规的非卷积人工神经网络中一样，完全连接层中的神经元与前一层中的所有激活都有联系。因此，它们的激活可以作为仿射变换来计算，也就是先乘以一个矩阵然后加上一个偏差(bias)偏移量(向量加上一个固定的或者学习来的偏差量)。

​ 讲了这么多，是不是已经懵了。

​ 不用担心， pytorch 已经帮我们把功能都给包装好了！

实验代码

# -*-coding: UTF-8 -*-

import torch
import torchvision
from torch.backends import cudnn
from torch.utils import data
import matplotlib.pyplot as plt
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from Artificial_Intelligence.experiment_7.net import Net

def train(epoch):
  network.train()
  for batch_idx, (data, target) in enumerate(train_loader):
    optimizer.zero_grad()
    output = network(data)
    loss = F.nll_loss(output, target)
    loss.backward()
    optimizer.step()
    if batch_idx % log_interval == 0:
      print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
        epoch, batch_idx * len(data), len(train_loader.dataset),
        100. * batch_idx / len(train_loader), loss.item()))
      train_losses.append(loss.item())
      train_counter.append(
        (batch_idx*64) + ((epoch-1)*len(train_loader.dataset)))
      torch.save(network.state_dict(), './results/model.pth')
      torch.save(optimizer.state_dict(), './results/optimizer.pth')


def test():
  network.eval()
  test_loss = 0
  correct = 0
  with torch.no_grad():
    for data, target in test_loader:
      output = network(data)
      test_loss += F.nll_loss(output, target, size_average=False).item()
      pred = output.data.max(1, keepdim=True)[1]
      correct += pred.eq(target.data.view_as(pred)).sum()
  test_loss /= len(test_loader.dataset)
  test_losses.append(test_loss)
  print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
    test_loss, correct, len(test_loader.dataset),
    100. * correct / len(test_loader.dataset)))



if __name__ == "__main__":
    n_epochs = 3
    batch_size_train = 64
    batch_size_test = 1000
    learning_rate = 0.01
    momentum = 0.5
    log_interval = 10

    random_seed = 1
    torch.backends.cudnn.enabled = False
    torch.manual_seed(random_seed)

    train_loader = torch.utils.data.DataLoader(
        torchvision.datasets.MNIST('./files/', train=True, download=True,
                                   transform=torchvision.transforms.Compose([
                                       torchvision.transforms.ToTensor(),
                                       torchvision.transforms.Normalize(
                                           (0.1307,), (0.3081,))
                                   ])),
        batch_size=batch_size_train, shuffle=True)

    test_loader = torch.utils.data.DataLoader(
        torchvision.datasets.MNIST('./files/', train=False, download=True,
                                   transform=torchvision.transforms.Compose([
                                       torchvision.transforms.ToTensor(),
                                       torchvision.transforms.Normalize(
                                           (0.1307,), (0.3081,))
                                   ])),
        batch_size=batch_size_test, shuffle=True)

    examples = enumerate(test_loader)
    batch_idx, (example_data, example_targets) = next(examples)

    print(example_data.shape)
    print(example_data)


    fig = plt.figure()
    for i in range(6):
        plt.subplot(2, 3, i + 1)
        plt.tight_layout()
        plt.imshow(example_data[i][0], cmap='gray', interpolation='none')
        plt.title("Ground Truth: {}".format(example_targets[i]))
        plt.xticks([])
        plt.yticks([])

    plt.show()

    network = Net()
    optimizer = optim.SGD(network.parameters(), lr=learning_rate,
                          momentum=momentum)

    train_losses = []
    train_counter = []
    test_losses = []
    test_counter = [i * len(train_loader.dataset) for i in range(n_epochs + 1)]

    test()
    for epoch in range(1, n_epochs + 1):
        train(epoch)
        test()

    fig = plt.figure()
    plt.plot(train_counter, train_losses, color='blue')
    plt.scatter(test_counter, test_losses, color='red')
    plt.legend(['Train Loss', 'Test Loss'], loc='upper right')
    plt.xlabel('number of training examples seen')
    plt.ylabel('negative log likelihood loss')

    plt.show()

    with torch.no_grad():
        output = network(example_data)

    fig = plt.figure()
    for i in range(6):
        plt.subplot(2, 3, i + 1)
        plt.tight_layout()
        plt.imshow(example_data[i][0], cmap='gray', interpolation='none')
        plt.title("Prediction: {}".format(
            output.data.max(1, keepdim=True)[1][i].item()))
        plt.xticks([])
        plt.yticks([])

    plt.show()

    continued_network = Net()
    continued_optimizer = optim.SGD(network.parameters(), lr=learning_rate,
                                    momentum=momentum)

    network_state_dict = torch.load("./results/model.pth")
    continued_network.load_state_dict(network_state_dict)

    optimizer_state_dict = torch.load("./results/optimizer.pth")
    continued_optimizer.load_state_dict(optimizer_state_dict)

    for i in range(4, 9):
        test_counter.append(i * len(train_loader.dataset))
        train(i)
        test()

    fig = plt.figure()
    plt.plot(train_counter, train_losses, color='blue')
    plt.scatter(test_counter, test_losses, color='red')
    plt.legend(['Train Loss', 'Test Loss'], loc='upper right')
    plt.xlabel('number of training examples seen')
    plt.ylabel('negative log likelihood loss')

    plt.show()

实验结果

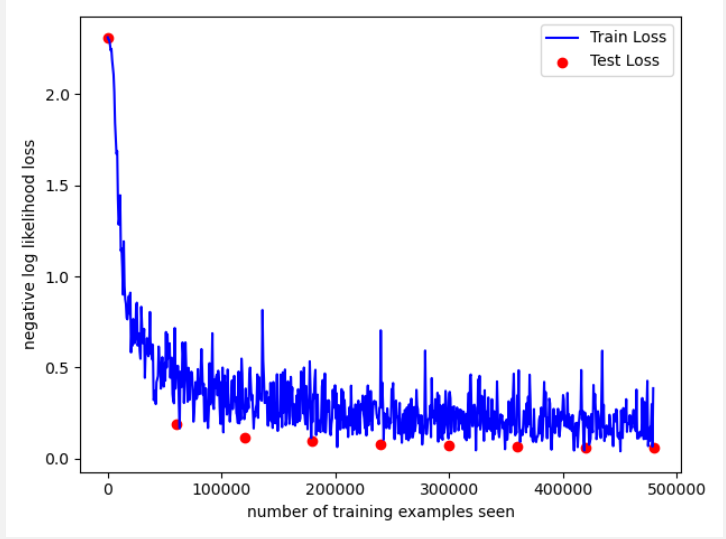
总结

​ 通过这次实验， 让我对神经网络和卷积神经网络有了一个更加深入的了解，尤其是卷积网络中的卷积层、池化层、全连接层等等，在这个整个实验过程当中，当遇到自己无法解决的问题的时候，可以通过上网查询相关资料或者咨询其他同学，通过这种方式，不仅仅可以巩固自己在课堂上所学的知识，还可以拓宽自己的知识面，了解到更多在课堂上并未提及的东西，受益匪浅。