13 Dec 2021 16075字 54分

启发式算法解决八数码难题

实验内容

用状态空间法解决八数码难题，采用2 种启发式搜索算法。

实验原理

启发式算法

启发式算法是相对于最优算法提出的。一个问题的最优算法是指求得该问题每个实例的最优解。启发式算法可以这样定义：一个基于直观或经验构造的算法，在可接受的花费（指计算时间、占用空间）下给出待解决组合优化问题每一个实例的一个可行解，该可行解与最优解的偏离成都不一定实现事先可以预计。

在某些情况下，特别是实际问题钟，最优算法的计算时间让人无法忍受，或者因问题的难度使其计算时间随问题规模的增加以指数速度增加，此时只能通过启发式算法求得问题的一个可行解。

利用启发式算法进行目标优化的一些优缺点如下：

优点	缺点
1.算法简单直观，易于修改	1. 不能保证为全局的最优解
2. 算法能够在可接受的时间内给出一个较优解	2. 算法不稳定，性能取决于具体问题和设计者经验

启发式算法的划分为如下三类： 简单启发式算法、 元启发式算法和超启发式算法。

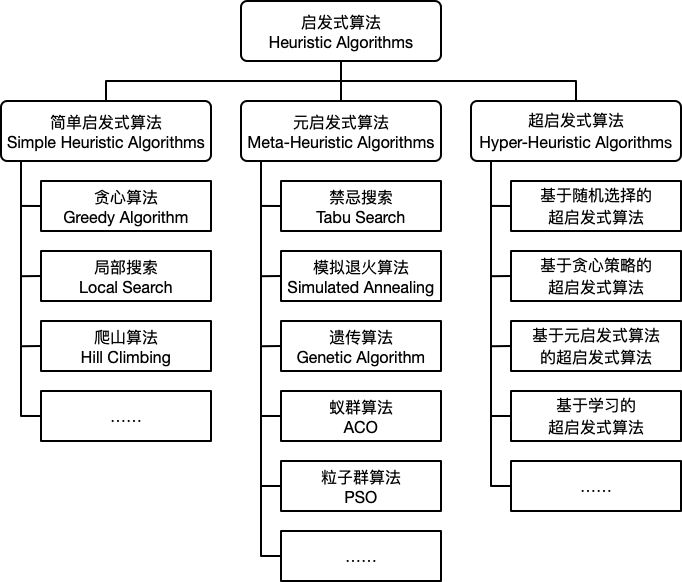
接下来对简单启发式算法进行一个简单的介绍：

简单启发式算法

贪心算法

贪心算法是指一种在求解问题时总是采取当前状态下最优的选择从而得到最优解的算法。贪心算法的基本步骤定义如下：

确定问题的最优子结构。
设计递归解，并保证在任一阶段，最优选择之一总是贪心选择。
实现基于贪心策略的递归算法，并转换成迭代算法。

对于利用贪心算法求解的问题需要包含如下两个重要的性质：

最优子结构性质。当一个问题具有最优子结构性质时，可用 动态规划 法求解，但有时用贪心算法求解会更加的简单有效。同时并非所有具有最优子结构性质的问题都可以利用贪心算法求解。
贪心选择性质。所求问题的整体最优解可以通过一系列局部最优的选择 (即贪心选择) 来达到。这是贪心算法可行的基本要素，也是贪心算法与动态规划算法的主要区别。

贪心算法和动态规划算法之间的差异如下表所示：

贪心算法	动态规划
每个阶段可以根据选择当前状态最优解快速的做出决策	每个阶段的选择建立在子问题的解之上
可以在子问题求解之前贪婪的做出选择	子问题需先进行求解
自顶向下的求解	自底向上的求解 (也可采用带备忘录的自顶向下方法)
通常情况下简单高效	效率可能比较低

局部搜索和爬山算法

局部搜索算法基于贪婪思想，从一个候选解开始，持续地在其邻域中搜索，直至邻域中没有更好的解。对于一个优化问题： $minf(x),x∈R^n$ 其中，$f(x)$ 为目标函数。搜索可以理解为从一个解移动到另一个解的过程，令 $s(x)$ 表示通过移动得到的一个解，$S(x)$ 为从当前解出发所有可能的解的集合 (邻域)，则局部搜索算法的步骤描述如下：

初始化一个可行解 $x$。
在当前解的邻域内选择一个移动后的解 $s(x)$，使得 $f(s(x))<f(x),s(x)∈S(x)$，如果不存在这样的解，则 x 为最优解，算法停止。
令 $x=s(x)$ ，重复步骤 2。

当我们的优化目标为最大化目标函数 $f(x)$ 时，这种局部搜索算法称之为爬山算法。

元启发式算法

禁忌搜索

禁忌搜索 (Tabu Search) 是由 Glover 提出的一种优化方法。禁忌搜索通过在解邻域内搜索更优的解的方式寻找目标的最优解，在搜索的过程中将搜索历史放入禁忌表 (Tabu List) 中从而避免重复搜索。禁忌表通过模仿人类的记忆功能，禁忌搜索因此得名。

在禁忌搜索算法中，禁忌表用于防止搜索过程出现循环，避免陷入局部最优。对于一个给定长度的禁忌表，随着新的禁忌对象的不断进入，旧的禁忌对象会逐步退出，从而可以重新被访问。禁忌表是禁忌搜索算法的核心，其功能同人类的短时记忆功能相似，因此又称之为“短期表”。

在某些特定的条件下，无论某个选择是否包含在禁忌表中，我们都接受这个选择并更新当前解和历史最优解，这个选择所满足的特定条件称之为渴望水平。

一个基本的禁忌搜索算法的步骤描述如下：

给定一个初始可行解，将禁忌表设置为空。
选择候选集中的最优解，若其满足渴望水平，则更新渴望水平和当前解；否则选择未被禁忌的最优解。
更新禁忌表。
判断是否满足停止条件，如果满足，则停止算法；否则转至步骤 2。

模拟退火

模拟退火 (Simulated Annealing) 是一种通过在邻域中寻找目标值相对小的状态从而求解全局最优的算法，现代的模拟退火是由 Kirkpatrick 等人于 1983 年提出 4。模拟退火算法源自于对热力学中退火过程的模拟，在给定一个初始温度下，通过不断降低温度，使得算法能够在多项式时间内得到一个近似最优解。

对于一个优化问题 $minf(x)$，模拟退火算法的步骤描述如下：

给定一个初始可行解 $x_0$，初始温度 $T_0$ 和终止温度 $T_f$，令迭代计数为 $k$。
随机选取一个邻域解 $x_k$，计算目标函数增量 $Δf=f(x_k)−f(x)$。若 $Δf<0$，则令 $x=x_k$；否则生成随机数 $ξ=U(0,1)$，若随机数小于转移概率 $P(Δf,T)$，则令 $x=x_k$。
降低温度 $T$。
若达到最大迭代次数 $k_{max}$ 或最低温度 $T_f$，则停止算法；否则转至步骤 2。

整个算法的伪代码如下：

在进行邻域搜索的过程中，当温度较高时，搜索的空间较大，反之搜索的空间较小。类似的，当 $Δf>0$ 时，转移概率的设置也同当前温度的大小成正比。常用的降温函数有两种：

$T_{k+1}=T_k∗r$，其中 $r∈(0.95,0.99)$，$r$ 设置的越大，温度下降越快。
$T_{k+1}=T_k−ΔT$，其中 $ΔT$ 为每一步温度的减少量。

初始温度和终止温度对算法的影响较大，相关参数设置的细节请参见参考文献。

模拟退火算法是对局部搜索和爬山算法的改进，我们通过如下示例对比两者之间的差异。假设目标函数如下：

(2)$f(x,y)=e^{−(x2+y2)}+2e^{−((x−1.7)2+(y−1.7)2)}$

优化问题定义为：

(3)$maxf(x,y),x∈[−2,4],y∈[−2,4]$

我们分别令初始解为 $(1.5,−1.5)$ 和 $(3.5,0.5)$，下图 (上) 为爬山算法的结果，下图 (下) 为模拟退火算法的结果。

其中，白色的大点为初始解位置，粉色的大点为求解的最优解位置，颜色从白到粉描述了迭代次数。从图中不难看出，由于局部最大值的存在，从不同的初始解出发，爬山算法容易陷入局部最大值，而模拟退火算法则相对稳定。

遗传算法

遗传算法 (Genetic Algorithm, GA) 是由 John Holland 提出，其学生 Goldberg 对整个算法进行了进一步完善。算法的整个思想来源于达尔文的进化论，其基本思想是根据问题的目标函数构造一个适应度函数 (Fitness Function)，对于种群中的每个个体 (即问题的一个解) 进行评估 (计算适应度)，选择，交叉和变异，通过多轮的繁殖选择适应度最好的个体作为问题的最优解。算法的整个流程如下所示：

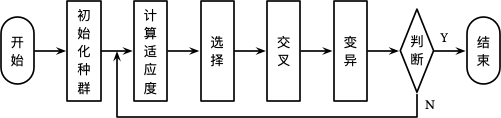
初始化种群

在初始化种群时，我们首先需要对每一个个体进行编码，常用的编码方式有二进制编码，实值编码，矩阵编码，树形编码等。以二进制为例 (如下不做特殊说明时均以二进制编码为例)，对于 $p∈{0,1,…,100}$ 中 $p_i=50$ 可以表示为：

(4)$x_i=50_{10}=0110010_2$

对于一个具体的问题，我们需要选择合适的编码方式对问题的解进行编码，编码后的个体可以称之为一个染色体。则一个染色体可以表示为：

(5)$x=(p_1,p_2,…,p_m)$

其中，$m$ 为染色体的长度或编码的位数。初始化种群个体共 $n$ 个，对于任意一个个体染色体的任意一位 $i$，随机生成一个随机数 $rand∈U(0,1)$，若 $rand>0.5$，则 $p_i=1$，否则 $p_i=0$。

计算适应度

适应度为评价个体优劣程度的函数 f(x)，通常为问题的目标函数，对最小化优化问题 $f(x)=−min∑L(\overline{y},y)$，对最大化优化问题 $f(x)=max∑L(\overline{y},y)$，其中 $L$ 为损失函数。

选择

对于种群中的每个个体，计算其适应度，记第 $i$ 个个体的适应度为 $F_i=f(x_i)$。则个体在一次选择中被选中的概率为： $P_i = \frac{F_i}{\sum_{i = 1}^{nn}F_i}$$ 为了保证种群的数量不变，我们需要重复 n 次选择过程，单次选择采用轮盘赌的方法。利用计算得到的被选中的概率计算每个个体的累积概率： $CP_0 = 0$

\[CP_i=\sum_{j= 1}^{i}P_i\]

交叉

交叉运算类似于染色体之间的交叉，常用的方法有单点交叉，多点交叉和均匀交叉等。

单点交叉：在染色体中选择一个切点，然后将其中一部分同另一个染色体的对应部分进行交换得到两个新的个体。交叉过程如下图所示：

多点交叉：在染色体中选择多个切点，对其任意两个切点之间部分以概率 Pc 进行交换，其中 Pc 为一个较大的值，例如 Pm=0.9。两点交叉过程如下图所示：

均匀交叉：染色体任意对应的位置以一定的概率进行交换得到新的个体。交叉过程如下图所示：

变异

变异即对于一个染色体的任意位置的值以一定的概率 Pm 发生变化，对于二进制编码来说即反转该位置的值。其中 Pm 为一个较小的值，例如 Pm=0.05。

小结

在整个遗传运算的过程中，不同的操作发挥着不同的作用：

选择：优胜劣汰，适者生存。
交叉：丰富种群，持续优化。
变异：随机扰动，避免局部最优。

除此之外，对于基本的遗传算法还有多种优化方法，例如：精英主义，即将每一代中的最优解原封不动的复制到下一代中，这保证了最优解可以存活到整个算法结束。

粒子群算法

Eberhart, R. 和 Kennedy, J. 于 1995 年提出了粒子群优化算法 10 11。粒子群算法模仿的是自然界中鸟群和鱼群等群体的行为，其基本原理描述如下：

一个由 m 个粒子 (Particle) 组成的群体 (Swarm) 在 D 维空间中飞行，每个粒子在搜索时，考虑自己历史搜索到的最优解和群体内 (或邻域内) 其他粒子历史搜索到的最优解，在此基础上进行位置 (状态，也就是解) 的变化。令第 i 个粒子的位置为 xi，速度为 vi，历史搜索的最优解对应的点为 pi，群体内 (或邻域内) 所有粒子历史搜索到的最优解对应的点为 pg，则粒子的位置和速度依据如下公式进行变化：

$v_i^{k+1}=ωv_i^k+c_1ξ(p_i^k−x_i^k)+c2η(p_g^k−x_i^k)$

$x_i^{k+1}=x_i^k+v_i^{k+1}$

其中，$ω$ 为惯性参数；$c_1$ 和 $c_2$ 为学习因子，其一般为正数，通常情况下等于 $2$；$ξ,η∈U[0,1]$。学习因子使得粒子具有自我总结和向群体中优秀个体学习的能力，从而向自己的历史最优点以及群体内或邻域内的最优点靠近。同时，粒子的速度被限制在一个最大速度 $V_{max}$ 范围内。

启发式算法对运算性能的影响

任何的搜索问题中，每个节点都有 $b$ 个选择以及到达目标的深度 $d$ ，一个毫无技巧的算法通常都要搜索 $b^{{d}}$ 个节点才能找到答案。启发式算法借由使用某种切割机制降低了分支因子$（branching\ factor）$以改进搜索效率，由 $b^d $ 降到较低的 $b`$ 分叉率可以用来定义启发式算法的偏序关系，例如：若在一个 $n$ 节点的搜索树上，$h_1(n)$的分叉率较 $h_2(n)$ 低，则$h_1(n)<h_2(n)$。启发式为每个要解决特定问题的搜索树的每个节点提供了较低的分叉率，因此它们拥有较佳效率的计算能力。

估价函数

估价函数，即估算节点希望程度的量度。

表示方法：$F(n)$，表示节点 $n$ 的估价函数值。

建立估价函数的一般方法：

• 提出任意节点与目标集之间的距离量度或差别量度。

• 在棋盘式的博弈和难题中根据棋局的某些特点来决定棋局的得分数。这些特点被认为与向目标节点前进一步的希望程度有关。

A*算法

估价函数

$f(n) = g(n) + h(n)$，其中， $g(n)$ 是对 $g^{(n)}$ 的估计， $g(n) >= g^{(n)}$，$h(n)$ 是 $h^{(n)}$ 的下界，即对所有的 n，$h(n) <= h^{(n)}$。

其中，$g^(n)$ 是从初始节点 $S_0 $ 到任意节点 $n$ 的一条最佳路径的代价，$h^(n)$ 是从节点 $n$ 到目标节点的一条最佳路径的代价。

定义1

在图搜索过程中，如果重排 $OPEN$ 表是依据$f(n)=g(n)+h(n)$ 进行的,则称该过程为A算法。

定义2

在A算法中,如果对所有的 $n$ 存在 $h(n)≤h(n)$ ,则称h(n)为h(n) 的下界,它表示某种偏于保守的估计

定义3

采用 $h^(n)$ 的下界$h(n)$为启发函数的 $A$ 算法，称为 $A$ 算法。

实验代码

根据函数判断初始情况是否可解。

def is_solvable():                  #判断初始情况是否有解
    state = Starting_states
    counts = 0
    for i in range(0, 9, 1):
        for j in range(0, 9, 1):
            if i == j or state[i] == 0 :
                continue
            if j > i and state[j] < state[i]:
                counts += 1

    if counts % 2 == 0:         #偶数
        return True
    else:
        return False

设置类 $Node$，当最后搜索到目标状态时，用于实现状态回溯。

class Node:
    __slots__ = "state", "previous", "next", "depth"

    def __init__(self, state, previous = None, next = None, depth = 0):
        self.state = state
        self.previous = previous
        self.next = next
        self.depth = depth

    def getPrevious(self):
        return self.previous

    def getNext(self):
        return self.next

    def getState(self):
        return self.state

    def set_next(self, next):
        self.next = next
        return

    def print_state(self):
        for i in range(0, 3, 1):
            for j in range(0, 3, 1):
                print(self.state[i * 3 + j], end = " ")

            print()
        print()
        return

$Stack$ 类，不过暂未使用。

class Stack:
    def __init__(self):
        self.data = []

    def __len__(self):
        pass

    def pop(self):
        pass

    def push(self):
        pass

    def isEmpty(self):
        pass

$Priority_queue$ 类，不过暂未使用。

class Priority_queue:

    def __init__(self):
        self.queue = []

    def add(self, key, state):
        #self.queue.append(self.Item(key, state))
        return

    def __len__(self):                                  #判断队列的长度
        return len(self.queue)

    def isEmpty(self):                                  #判断是否为空
        return len(self.queue) == 0

    def upheap(self):                                   #整体排序不可取，可能会导致前后顺序混乱！
        pass

Item 类，不过并未使用。（好像

class Item:
    __slots__ = "key", "node"

    def __init__(self, key, node):
        self.key = key
        self.node = node


    def getState(self):
        return self.node.getState()

通过有序搜索来寻找路径。

def findPath1():
    #通过有序搜索进行路径的寻找      无递归 DFS    栈栈栈栈栈栈
    depth = 0
    start_node = Node(Starting_states, None, Node, depth)
    start_item = Item(0, start_node)
    reachable.append(start_item)

    while len(reachable) != 0:
        item = reachable.pop(0)

        #print(item.node.state)
        #item.node.print_state()

        if item.node.depth >= 20:
            continue


        if isDestinationStates(item.getState()):            #找到目标状态
            print("找到目标状态")
            print(item.node.print_state())

            # -----------进行路径的回溯------------------------#
            path = []
            node = item.node
            destinate_states = item.getState()
            while True:
                if node.previous is not None:
                    # path.append(node.previous.state)
                    path.insert(0, node.previous.state)
                else:
                    break

                node = node.previous

            path.append(destinate_states)

            print("搜索的路径是：")
            for each in path:
                printState(each)
                print("⬇⬇⬇⬇⬇⬇")

            # ----------------------------------------------#

            return


        next_states = generateNextStates1(item.getState())
        next_items = []
        while len(next_states) != 0:
            next_state = next_states.pop(0)
            #node.next = next_state
            item.node.set_next(next_state)
            value = evaluateState1(next_state, item.node.depth + 1)
            next_node = Node(next_state,previous = item.node,next = None, depth = item.node.depth + 1)

            next_item = Item(value, next_node)
            next_items.append(next_item)

        #next_items = sorted(state = next_items, key=lambda x:x.key, reverse=False)
        #next_items = sorted(next_items, key = lambda x:x.key, reverse = True)       #以从大到小的顺序进行排序，插入队列时才能保证VALUE
                                                                                    #值最小的在最前面
        for item in next_items:
            print(item.key)
            print(item.node.depth)
            item.node.print_state()
            #reachable.insert(0, item)
            reachable.append(item)

        reachable = sorted(next_items, key=lambda x: x.key, reverse=False)
        print("-----------------------------------------")
    print("未找到目标状态")
    return

通过 A * 算法来搜寻路径。

def findPath2(reachable):
    # 通过 A * 算法 进行路径的寻找      无递归 DFS    栈栈栈栈栈栈
    depth = 0
    start_node = Node(Starting_states, None, Node, depth)
    start_item = Item(0, start_node)
    reachable.append(start_item)

    while len(reachable) != 0:
        item = reachable.pop(0)

        # print(item.node.state)
        # item.node.print_state()

        if item.node.depth >= 10:
            continue
        # depth += 1
        # print(type(node))
        if isDestinationStates(item.getState()):  # 找到目标状态
            print("找到目标状态")
            print(item.node.print_state())

            #-----------进行路径的回溯------------------------#
            path = []
            node = item.node
            destinate_states = item.getState()
            while True:
                if node.previous is not None:
                    #path.append(node.previous.state)
                    path.insert(0, node.previous.state)
                else:
                    break

                node = node.previous

            path.append(destinate_states)

            print("搜索的路径是：")
            for each in path:
                printState(each)
                print("⬇⬇⬇⬇⬇⬇")


            #----------------------------------------------#
            return

        next_states = generateNextStates1(item.getState())
        next_items = []
        while len(next_states) != 0:
            next_state = next_states.pop(0)
            # node.next = next_state
            item.node.set_next(next_state)
            value = evaluateState2(next_state, item.node.depth + 1)
            next_node = Node(next_state, previous=item.node, next=None, depth=item.node.depth + 1)

            next_item = Item(value, next_node)
            next_items.append(next_item)

        # next_items = sorted(state = next_items, key=lambda x:x.key, reverse=False)
        #next_items = sorted(next_items, key=lambda x: x.key, reverse=True)          #以从大到小的顺序进行排序，插入队列时才能保证VALUE
                                                                                    #值最小的在最前面

        for item in next_items:
            print(item.key)
            print(item.node.depth)
            item.node.print_state()
            #reachable.insert(0, item)
            reachable.append(item)

        reachable = sorted(next_items, key = lambda x: x.key, reverse = False)
        for i in reachable:
            print(i.key)
        print("-----------------------------------------")
    print("未找到目标状态")
    return

全部代码如下：

# -*-coding:UTF-8 -*-

Starting_states = [2, 8, 3,
                   1, 6, 4,
                   7, 0, 5]

ending_states =    [1, 2, 3,
                    8, 0, 4,
                    7, 6, 5]

move_direction = ['up', 'down', 'left', 'right']
reachable = []
explored = []

def is_solvable():                  #判断初始情况是否有解
    state = Starting_states
    counts = 0
    for i in range(0, 9, 1):
        for j in range(0, 9, 1):
            if i == j or state[i] == 0 :
                continue
            if j > i and state[j] < state[i]:
                counts += 1

    if counts % 2 == 0:         #偶数
        return True
    else:
        return False






class Node:
    __slots__ = "state", "previous", "next", "depth"

    def __init__(self, state, previous = None, next = None, depth = 0):
        self.state = state
        self.previous = previous
        self.next = next
        self.depth = depth

    def getPrevious(self):
        return self.previous

    def getNext(self):
        return self.next

    def getState(self):
        return self.state

    def set_next(self, next):
        self.next = next
        return

    def print_state(self):
        for i in range(0, 3, 1):
            for j in range(0, 3, 1):
                print(self.state[i * 3 + j], end = " ")

            print()
        print()
        return

class Stack:
    def __init__(self):
        self.data = []

    def __len__(self):
        pass

    def pop(self):
        pass

    def push(self):
        pass

    def isEmpty(self):
        pass


class Priority_queue:

    def __init__(self):
        self.queue = []

    def add(self, key, state):
        #self.queue.append(self.Item(key, state))
        return

    def __len__(self):                                  #判断队列的长度
        return len(self.queue)

    def isEmpty(self):                                  #判断是否为空
        return len(self.queue) == 0

    def upheap(self):                                   #整体排序不可取，可能会导致前后顺序混乱！
        pass



class Item:
    __slots__ = "key", "node"

    def __init__(self, key, node):
        self.key = key
        self.node = node


    def getState(self):
        return self.node.getState()





def isDestinationStates(state):

    for i in range(0, 3, 1):
        for j in range(0, 3, 1):
            if state[i * 3 + j] != ending_states[i * 3 + j]:
                return False

    return True

old_states = []
def generateNextStates1(states):
    temp_arr = []
    temp_arr = states.copy()
    index = states.index(0)
    index_i = index // 3
    index_j = index % 3
    #print(index_i, index_j)
    #print(states[index_i * 3 + index_j])
    results = []
    temp = 0
    global temp_y
    global temp_x
    if index_i - 1 >= 0 :  # 上

        temp = temp_arr[index_i * 3 + index_j]
        temp_arr[index_i * 3 + index_j] = temp_arr[(index_i - 1) * 3 + index_j]
        temp_arr[(index_i - 1) * 3 + index_j] = temp
        if temp_arr in old_states:
            pass
        else:
            results.append(temp_arr)
            old_states.append(temp_arr)
        #results.append(temp_arr)


    temp_arr = states.copy()
    if index_i + 1 < 3 :  # 下
        temp_arr[index_i + index_j], temp_arr[(index_i + 1) * 3 + index_j] = temp_arr[(index_i + 1) * 3 + index_j], \
                                                                             temp_arr[index_i + index_j]
        if temp_arr in old_states:
            pass
        else:
            results.append(temp_arr)
            old_states.append(temp_arr)
        #results.append(temp_arr)

    temp_arr = states.copy()
    if index_j - 1 >= 0:  # 左
        temp_arr[index_i * 3 + index_j], temp_arr[index_i * 3 + index_j - 1] = temp_arr[index_i * 3 + index_j - 1], \
                                                                               temp_arr[index_i * 3 + index_j]
        if temp_arr in old_states:
            pass
        else:
            results.append(temp_arr)
            old_states.append(temp_arr)
        #results.append(temp_arr)

    temp_arr = states.copy()
    if index_j + 1 < 3 :  # 右
        temp_arr[index_i * 3 + index_j], temp_arr[index_i * 3 + index_j + 1] = temp_arr[index_i * 3 + index_j + 1], \
                                                                               temp_arr[index_i * 3 + index_j]
        if temp_arr in old_states:
            pass
        else:
            results.append(temp_arr)
            old_states.append(temp_arr)
        #results.append(temp_arr)

    #temp_x = index_i
    #temp_y = index_j  # 记录当前的位置， 避免重复
    #print()
    return results


def evaluateState1(state, depth):
    values = 0
    for i in range(0, 3, 1):
        for j in range(0, 3, 1):
            if state[i * 3 + j] != ending_states[i * 3 + j]:        #当前节点不在位的将牌数
                values += 1

    values += depth                 #深度
    return values


def findPath1():
    #通过有序搜索进行路径的寻找      无递归 DFS    栈栈栈栈栈栈
    depth = 0
    start_node = Node(Starting_states, None, Node, depth)
    start_item = Item(0, start_node)
    reachable.append(start_item)

    while len(reachable) != 0:
        item = reachable.pop(0)

        #print(item.node.state)
        #item.node.print_state()

        if item.node.depth >= 20:
            continue


        if isDestinationStates(item.getState()):            #找到目标状态
            print("找到目标状态")
            print(item.node.print_state())

            # -----------进行路径的回溯------------------------#
            path = []
            node = item.node
            destinate_states = item.getState()
            while True:
                if node.previous is not None:
                    # path.append(node.previous.state)
                    path.insert(0, node.previous.state)
                else:
                    break

                node = node.previous

            path.append(destinate_states)

            print("搜索的路径是：")
            for each in path:
                printState(each)
                print("⬇⬇⬇⬇⬇⬇")

            # ----------------------------------------------#

            return


        next_states = generateNextStates1(item.getState())
        next_items = []
        while len(next_states) != 0:
            next_state = next_states.pop(0)
            #node.next = next_state
            item.node.set_next(next_state)
            value = evaluateState1(next_state, item.node.depth + 1)
            next_node = Node(next_state,previous = item.node,next = None, depth = item.node.depth + 1)

            next_item = Item(value, next_node)
            next_items.append(next_item)

        #next_items = sorted(state = next_items, key=lambda x:x.key, reverse=False)
        #next_items = sorted(next_items, key = lambda x:x.key, reverse = True)       #以从大到小的顺序进行排序，插入队列时才能保证VALUE
                                                                                    #值最小的在最前面
        for item in next_items:
            print(item.key)
            print(item.node.depth)
            item.node.print_state()
            #reachable.insert(0, item)
            reachable.append(item)

        reachable = sorted(next_items, key=lambda x: x.key, reverse=False)
        print("-----------------------------------------")
    print("未找到目标状态")
    return


def evaluateState2(state, depth):
    value = 0
    for i in range(0, 3, 1):
        for j in range(0, 3, 1):
            index = ending_states.index(state[i * 3 + j])
            value += abs((index // 3 - i) ** 2 + (index % 3 - j) ** 2)          #每一将牌与目标位置之间的距离总和

    value += depth
    return value

def printState(state):
    for i in range(0, 3, 1):
        print("[ ", end="")
        for j in range(0, 3, 1):
            print(state[i * 3 + j], end = " ")
        print("]")


def findPath2(reachable):
    # 通过 A * 算法 进行路径的寻找      无递归 DFS    栈栈栈栈栈栈
    depth = 0
    start_node = Node(Starting_states, None, Node, depth)
    start_item = Item(0, start_node)
    reachable.append(start_item)

    while len(reachable) != 0:
        item = reachable.pop(0)

        # print(item.node.state)
        # item.node.print_state()

        if item.node.depth >= 10:
            continue
        # depth += 1
        # print(type(node))
        if isDestinationStates(item.getState()):  # 找到目标状态
            print("找到目标状态")
            print(item.node.print_state())

            #-----------进行路径的回溯------------------------#
            path = []
            node = item.node
            destinate_states = item.getState()
            while True:
                if node.previous is not None:
                    #path.append(node.previous.state)
                    path.insert(0, node.previous.state)
                else:
                    break

                node = node.previous

            path.append(destinate_states)

            print("搜索的路径是：")
            for each in path:
                printState(each)
                print("⬇⬇⬇⬇⬇⬇")


            #----------------------------------------------#
            return

        next_states = generateNextStates1(item.getState())
        next_items = []
        while len(next_states) != 0:
            next_state = next_states.pop(0)
            # node.next = next_state
            item.node.set_next(next_state)
            value = evaluateState2(next_state, item.node.depth + 1)
            next_node = Node(next_state, previous=item.node, next=None, depth=item.node.depth + 1)

            next_item = Item(value, next_node)
            next_items.append(next_item)

        # next_items = sorted(state = next_items, key=lambda x:x.key, reverse=False)
        #next_items = sorted(next_items, key=lambda x: x.key, reverse=True)          #以从大到小的顺序进行排序，插入队列时才能保证VALUE
                                                                                    #值最小的在最前面

        for item in next_items:
            print(item.key)
            print(item.node.depth)
            item.node.print_state()
            #reachable.insert(0, item)
            reachable.append(item)

        reachable = sorted(next_items, key = lambda x: x.key, reverse = False)
        for i in reachable:
            print(i.key)
        print("-----------------------------------------")
    print("未找到目标状态")
    return





if __name__ == "__main__":


    #findPath1()
    findPath2(reachable)




    pass

实验结果

结果如下图所示：

总结

通过这次实验，使我对启发式算法有了一个简单的了解，了解到了启发式算法分为：简单启发式算法，元启发式算法，和超启发式算法，并且学会了 A* 算法和 A 算法的具体使用方法，并且对贪心算法、爬山算法等有了一个大概的认知，收获颇丰。