数据挖掘实验
一、实验目的
掌握 $SVM$ 算法的原理。
二、实验要求
(1)掌握 $SVM$ 算法的基本思想。
(2)熟练使用 $Python$ 或其他工具实现 $SVM$ 算法。
三、实验器材
(1)计算机一台。
(2)$Python$ 或其他编程工具。
四、实验内容
支持向量机
定义
在机器学习中,支持向量机( $SVM$, 又名支持向量网络)是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。给定一组训练实例,每个训练实例被标记为属于两个类别中的一个或另一个,$SVM$ 训练算法将创建一个将新的实例分配给两个类别之一的模型,使其成为非概率二元线性分类器。$SVM$ 模型是将实例表示为空间中的点,这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后,将新的实例映射到同一空间,并基于它们落在间隔的哪一侧来预测所属类别。
除了进行线性分类之外,$SVM$ 还可以使用所谓的核技巧有效地进行非线性分类,将其输入隐式映射到高维特征空间中。
当数据未被标记时,不能进行监督式学习,需要使用非监督式学习,它会尝试找出数据到簇的自然聚类,并将新数据映射到这些已形成的簇。将支持向量机改进的聚类算法被称为支持向量聚类,当数据未被标记或者仅一些数据被标记时,支持向量聚类经常在工业应用中用作分类步骤的预处理。
算法原理
对于支持向量机来说,数据点若是维向量,我们用
维的超平面来分开这些点。但是可能有许多超平面可以把数据分类。最佳超平面的一个合理选择就是以最大间隔把两个类分开的超平面。因此,$SVM$ 选择能够使离超平面最近的数据点的到超平面距离最大的超平面。
以上介绍的 $SVM$ 只能解决线性可分的问题,为了解决更加复杂的问题,支持向量机学习方法有一些由简至繁的模型。
线性可分SVM—–硬间隔
考虑到如下形式构成的线性可分的训练集: \((X_1,\ y_1),\ (X_2,\ y_2),.......,(X_n,\ y_n)\) 其中 $X_i$ 是一个含有 $d$ 个元素的列向量,即 $X_i ∈ R^d$ ,$y_i$ 是标量, $y ∈ +1,-1$,$y_i = +1$ 时表示 $X_i$ 属于正类别,$y_i = -1$ 时表示 $X_i$ 属于负类别。
超平面与间隔
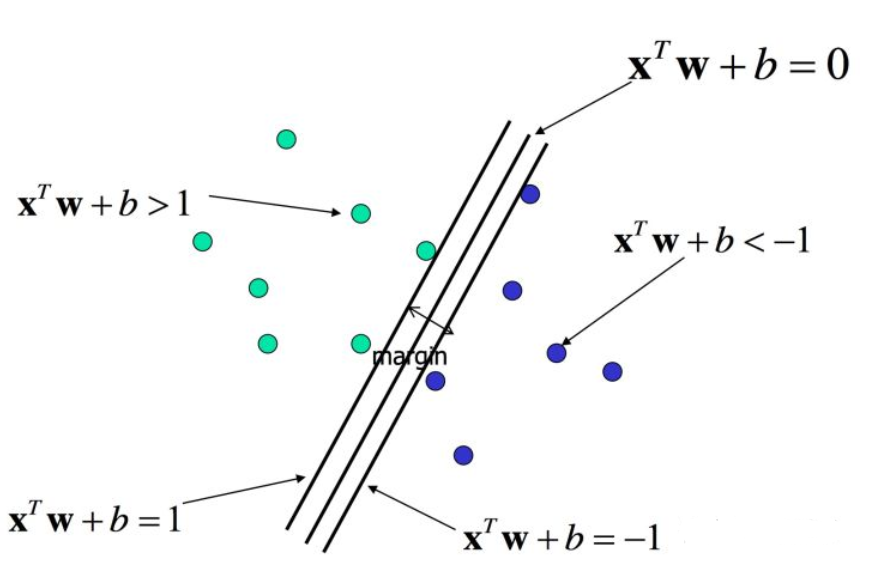
一个超平面由法向量 $W$ 和截距 $b$ 决定,其方程为 $X^{T}W + b = 0$ ,可以规定法向量指向的一侧为正类,另一侧为负类。
为了找到最大的间隔超平面(避免由于数据噪音而导致分类错误),我们可以选择分离两类数据的两个超平面,使得它们之间的距离尽可能大。在这两个超平面范围内的区域称为 ”间隔“,最大间隔超平面就是位于它们正中间的超平面。
间隔最大化
将数学中求两条平行直线的距离公式推广到高维即可求得如下的式子: \(margin = ρ\ =\ \frac{2}{||W||}\) 若要使得 $ρ$ 最大,即数学表达就是: \(\mathop{min}\limits_{W,b}J(W) = \mathop{min}\limits_{W, b}\frac{1}{2}||W||^2\)
\[s.t.\ \ \ y_i(X_i^TW +b)\ >=\ 1,i\ =\ 1,2,......n.\]支持向量
在线性可分的情况下,训练数据集中的样本点与分离超平面距离最近的数据点称为支持向量(support vector),支持向量是满足以下式子的点: \(y_i(X_i^TW\ +\ b)\ =\ 1\) 大致如下图所示:
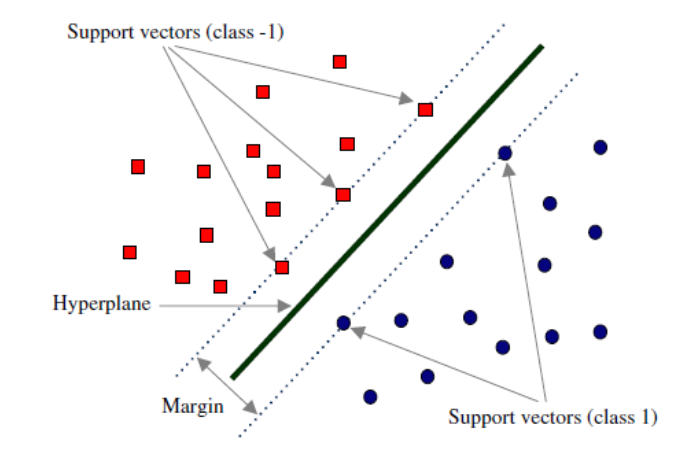
在决定最佳超平面时只有支持向量起作用,而其他数据点并不起作用(具体推导见2.4节最后)。如果移动非支持向量,甚至删除非支持向量都不会对最优超平面产生任何影响。也即支持向量对模型起着决定性的作用,这也是“支持向量机”名称的由来。
对偶问题
在求解间隔最大化问题时,可以通过拉格朗日乘子法构造拉格朗日函数,再通过求解其对偶问题来得到原始问题的最优解。转化为对偶问题来求解的原因是:
-
对偶问题更易求解,由下文知对偶问题只需优化一个变量 $α$ 且约束条件更简单;
-
能更加自然地引入核函数,进而推广到非线性问题。
拉格朗日函数为: \(L(W,b,α)=\frac{1}{2}||W||^2-\sum_{i=1}^{n}α_{i}[y_i(X^T_iW+b)-1]\) 具体的推导过程不再进行阐述了。(太复杂
线性SVM—–软间隔
存在一种情况,即不存在一个超平面可以将两类数据给分开。
软间隔最大化
解决这种问题的一个办法是允许 $SVM$ 在少量样本上出错,即将之前的硬间隔最大化条件放宽一点,为此引入”软间隔“的概念,即允许少量样本不满足下式约束: \(y_i(X^T_iW\ +\ b)>=\ 1\) 为了使得不满足上述条件的样本点尽可能的减少,我们需要在优化的目标函数里面新增一个对这些点的惩罚项。其中,最常用的是 $hinge$ 损失: \(l_{hinge}(Z)\ =\ max(0,1\ -\ Z)\) 即若样本点满足条件损失就是 $0$,否则损失就是 $1 - Z$ ,则优化目标变成: \(\mathop{min}\limits_{W, b}\frac{1}{2}||W||^2 + C\sum_{i=1}^{n}max(0,1-y_i(X^T_iW +b))\) 其中, $C$ 称为惩罚参数, $C$ 越小时对误分类惩罚越小,越大时对误分类惩罚越大,当 $C$ 取正无穷时就变成了硬间隔优化。实际应用时我们需要合理的选取 $C$, $C$ 越小越容易发生欠拟合,$C$ 越大越容易发生过拟合。
非线性SVM
在前面所介绍的都是线性问题,但是我们也经常会遇见非线性问题,因此需要用到核技巧 $(kernel trick)$ 将线性支持向量机推广到非线性支持向量机。需要注意的是,不仅仅是 $SVM$,许多线性模型都可以用核技巧推广到非线性模型,例如核线性判别分析 $(KLDA)$。
核函数
核技巧的基本思路分为两步:1. 使用一个变换将原空间的数据映射到新空间(例如更高维甚至无穷维的空间)2.然后再新空间里使用线性方法从训练数据中学习得到模型。
核函数的定义:
设 $X$ 是输入空间(欧式空间的 $R^n$ 子集或离散集合),又设 $H$ 是特征空间,如果存在一个 $X$ 到 $ H$ 的映射$ F(x):X—>H$ 使得对于所有的 $x$,$Z ∈ X$,函数 $K(x,z)$ 满足条件 $K(x,z)=F(x)·F(z)$ 则称 $K(x,z)$ 为核函数,$F(x)$ 为映射函数,式中 $F(x)·F(z)$ 为 $F(x)$ 和 $F(z)$ 的内积。
通常,直接计算 $K(x,z)$ 比较容易而通过 $F(x)$ 和 $F(z)$ 计算 $K(x,z)$ 并不容易。而幸运的是,在线性支持向量机的对偶问题中,无论是目标函数还是决策函数都只涉及到输入样本与样本之间的內积,因此我们不需要显式地定义映射 $F(x)$ 是什么而只需事先定义核函数 $K(x,z)$ 即可。也就是说,在核函数 $K(x,z)$ 给定的情况下,可以利用解线性问题的方法求解非线性问题的支持向量机,此过程是隐式地在特征空间中进行的。
正定核
通常情况下所说的核函数就是正定核函数,在实际问题中我们一般会使用已有的核函数,下面给出一些常用的核函数。
多项式核函数$(polynomial\ kernel\ function)$ $K(x,z)=(xz+1)^p$
| 高斯核函数$(Guassian\ kernel\ function)$ $K(x,z) =exp(-\frac{ | x-z | ^2}{2ρ^2})$ |
非线性支持向量机
利用核技巧可以很简单地把线性支持向量机扩展到非线性支持向量机,只需将线性支持向量机中的内积换成核函数即可。 下面简述非线性支持向量机学习算法。
首先取适当的核函数 $K(x,z)$ 和适当的参数 $C$,构造最优化问题: \(min\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}α_iα_jy_iy_jK(X_i,X_j)\ -\ \sum_{i=1}^nα_i\)
\[s.t.\ \ \sum_{i=1}^{n}α_iy_i\ =\ 0 ,0 <=α_i <=C,i=1,2,.....,n.\] 再利用现成的二次规划问题求解算法或者 $SMO$ 算法求得最优解 $\hat{α}$。
选择 $\hat{a}$ 的一个满足 $0<\hat{a_j}<C$ 的分量 $\hat{a_j}$,计算: \(\hat{b}\ =\ y_j-\sum_{i∈SV}\hat{a_i}y_iK(X_j,X_i)\) 构造决策函数: \(f(x)=sign(\sum_{i∈SV}\hat{a_i}y_jK(X_j,X_i)+\hat{b})\)
SMO算法
输入:训练数据集 $T={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)}$ \(x_i ∈ X = R^n,y_i ∈ Y = \{+1,-1\},i = 1,2,...,N,精度\)
- 取初值 $α^{(0)} = 0$,令 $k = 0$。
- 选取优化变量 $α_1^k,α_2^k$,解析求解两个变量的最优化问题,求得最优解 $α_1^{k+1},a_2^{k+1}$
- ,更新 $α$ 为 $α^{k+1}$。
- 若在精度范围内满足停机条件,则转4,否则,令 $k=k+1$ ,转2。
- 取$\hat{α}=α^{k+1}$ 。
应用
$SVM$ 的主要思想可以概括为如下两点:
-
它是针对线性可分的情况进行分析的。对于线性不可分的情况,通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间,使其线性可分,从而使得在高维特征空间中采用线性算法对样本的非线性特征进行线性分析成为可能。
-
它基于结构风险最小化理论,在特征空间中构建最优分类面,使得学习器能够得到全局最优化,并且使整个样本空间的期望风险以某个概率满足一定上界。
从上面的两点基本思想来看,$SVM$ 没有使用传统的推导过程,简化了通常的分类和回归等问题;少数的支持向量确定了 $SVM$ 的最终决策函数,计算的复杂性取决于支持向量,而不是整个样本空间,这就可以避免“维数灾难”。少数支持向量决定了最终结果,这不但可以帮助我们抓住关键样本,而且注定了该方法不但算法简单,而且具有较好的“鲁棒”性。
人脸检测、验证和识别
$Osuna$ 最早将 $SVM$ 应用于人脸检测,取得了较好的效果。其方法是直接训练非线性 $SVM$ 分类器完成人脸与非人脸的分类。由于 $SVM$ 的训练需要大量的存储空间,并且非线性 $SVM$ 分类器需要较多的支持向量,速度很慢,因此,他提出了一种层次性结构的 $SVM$ 分类器,它由一个线性 $SVM$ 的组合和一个非线性 $SVM$ 组成。检测时,由前者快速排除掉图像中绝大部分背景窗日,而后者只需对少量的候选区域做出确认。
说话人/语音识别
说话语音识别属于连续输入信号的分类问题, $SVM$ 是一个很好的分类器,但不适合连续输入样本。为此,引入了隐式马尔可夫模型 $HMM$ ,建立了 $SVM$ 和 $HMM$ 的混合模型。$HMM$ 适合处理连续信号,而 $SVM$ 适合分类问题;$HMM$ 的结果反映了同类样本的相似度,而 $SVM$ 的输出结果则体现了异类样本间的差异。为了方便与 $HMM$ 组成混合模型,需要首先将 $SVM$ 的输出形式改为概率输出。
文字/手写体识别
贝尔实验室对美国邮政手写数字库进行的实验中,人工识别平均错误率为 $2.500$,专门针对该特定问题设计的5层神经网络错误率为 $5.100$ (其中利用了大量先验知识),而用 $3$ 种 $SVM$ 方法(采用 $3$ 种核函数)得到的错误率分别为 $2.000$、$2.1\%$ 和 $2.200$,且 $SVM$ 是直接采用 $16X16$ 的字符点阵作为输入的,表明了 $SVM$ 的优越性能。
图像处理
图像过滤
一般的针对互联网色情图像的过滤软件主要采用网址库的形式封锁色情网址或采用人工智能方法对接收到的中、英文信息进行分析甄别。学者们提出了一种多层次特定类型图像过滤法,即综合肤色模型检验、支持向量机分类和最近邻方法校验的多层系图像处理框架,此方法能够达到 $85\%$ 以上的准确率。
视频字幕提取
视频字幕蕴含了丰富的语义,可用于对相应视频流进行高级语义标注。研究人员提出并实践了基于 $SVM$ 的视频字幕自动定位和提取的方法,该方法首先将原始图像的帧分割为 $N*N$ 的子块,提取每个子块的灰度特征,然后使用预先训练好的 $SVWM$ 分类机进行字幕子块和非字幕子块的分类,最后结合金字塔模型和后期处理,实现视频图像字幕区域的自动定位提取。
图像分类和检索
由于计算机自动抽取的图像特征和人所理解的语义间存在巨大差异,图像检索的结果难以令人满意。近年来出现了相关反馈方法,以 $SVM$ 为分类器,在每次反馈中对用户标记的正例和反例样本进行学习,并根据学习所得的模型进行检索。相关研究人员使用了由 $9918$ 幅图像组成的图像库进行了实验,结果表明,这种方法在训练样本有限的情况下具有良好的泛化功能。
优点
- 由于 $SVM$ 是一个凸优化问题,所以求得的解一定是全局最优而不是局部最优。
- 不仅适用于线性还适用于非线性问题(用核技巧)。
- 拥有高维样本空间的数据也能用 $SVM$,这是因为数据集的复杂度只取决于支持向量而不是数据集的维度,这在某种意义上避免了“维数灾难”。
- 理论基础比较完善(例如神经网络就更像一个黑盒子)。
缺点
- 二次规划问题求解将涉及 $m$ 阶矩阵的计算($m$ 为样本的个数), 因此 $SVM$ 不适用于超大数据集。($SMO$ 算法可以缓解这个问题)。
-
只适用于二分类问题。($SVM$ 的推广 $SVR$ 也适用于回归问题;可以通过多个$SVM$ 的组合来解决多分类问题)。
- 当观测样本很多时,效率并不是很高。
- 对非线性问题没有通用解决方案,有时候很难找到一个合适的核函数。
- 对于核函数的高维映射解释力不强,尤其是径向基函数。
- 常规 $SVM$ 只支持二分类。
数据集的选取
获取本地路径,此处使用的是 $iris$,如有需要可以去网上下载。
data_path = './iris.data' # 数据文件的路径
对本地文件进行加载,并进行一定的处理。
def iris_type(s):
# print(type(s))
#字符串加个b是指btypes 字节串类型
it = {b'Iris-setosa':0, b'Iris-versicolor':1, b'Iris-virginica':2}
return it[s]
data = np.loadtxt(data_path, # 数据文件路径
dtype=float, # 数据类型
delimiter=',', # 数据分隔符
converters={4: iris_type}) # 将第5列使用函数iris_type进行转换
核函数的选择
此处实验分别采用 线性核 和 高斯核对数据进行测试。
def classifier():
#clf = svm.SVC(C=0.8,kernel='rbf', gamma=50,decision_function_shape='ovr')
clf = svm.SVC(C=0.5, #误差项惩罚系数,默认值是1
kernel='linear', #线性核 kenrel="rbf":高斯核
decision_function_shape='ovr') #决策函数
def classifier():
#clf = svm.SVC(C=0.8,kernel='rbf', gamma=50,decision_function_shape='ovr')
clf = svm.SVC(C=0.5, #误差项惩罚系数,默认值是1
kernel='rbf', #线性核 kenrel="rbf":高斯核
decision_function_shape='ovr') #决策函数
训练和测试数据集的准确率为
其下代码对测试数据集和训练数据集的正确率进行一个计算,主要调用的是 $sklearn$ 包中 $ svm$ 里的内置函数。
def print_accuracy(clf,x_train,y_train,x_test,y_test):
#分别打印训练集和测试集的准确率 score(x_train,y_train):表示输出x_train,y_train在模型上的准确率
print('trianing prediction:%.3f' %(clf.score(x_train, y_train)))
print('test data prediction:%.3f' %(clf.score(x_test, y_test)))
#原始结果与预测结果进行对比 predict()表示对x_train样本进行预测,返回样本类别
show_accuracy(clf.predict(x_train), y_train, 'traing data')
show_accuracy(clf.predict(x_test), y_test, 'testing data')
#计算决策函数的值,表示x到各分割平面的距离,3类,所以有3个决策函数,不同的多类情况有不同的决策函数?
print('decision_function:\n', clf.decision_function(x_train))
def show_accuracy(a, b, tip):
acc = a.ravel() == b.ravel()
print('%s Accuracy:%.3f' %(tip, np.mean(acc)))
结果如下:
高斯核

线性核

可视化图
可视化图像的绘制。
def draw(clf, x):
iris_feature = 'sepal length', 'sepal width', 'petal lenght', 'petal width'
# 开始画图
x1_min, x1_max = x[:, 0].min(), x[:, 0].max() #第0列的范围
x2_min, x2_max = x[:, 1].min(), x[:, 1].max() #第1列的范围
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j] #生成网格采样点 开始坐标:结束坐标(不包括):步长
#flat将二维数组转换成1个1维的迭代器,然后把x1和x2的所有可能值给匹配成为样本点
grid_test = np.stack((x1.flat, x2.flat), axis=1) #stack():沿着新的轴加入一系列数组,竖着(按列)增加两个数组,grid_test的shape:(40000, 2)
print('grid_test:\n', grid_test)
# 输出样本到决策面的距离
z = clf.decision_function(grid_test)
print('the distance to decision plane:\n', z)
grid_hat = clf.predict(grid_test) # 预测分类值 得到【0,0.。。。2,2,2】
print('grid_hat:\n', grid_hat)
grid_hat = grid_hat.reshape(x1.shape) # reshape grid_hat和x1形状一致
#若3*3矩阵e,则e.shape()为3*3,表示3行3列
#light是网格测试点的配色,相当于背景
#dark是样本点的配色
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])
#画出所有网格样本点被判断为的分类,作为背景 即背景的不同颜色
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light) # pcolormesh(x,y,z,cmap)这里参数代入
# x1,x2,grid_hat,cmap=cm_light绘制的是背景。
#squeeze()把y的个数为1的维度去掉,也就是变成一维。
plt.scatter(x[:, 0], x[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark) # 样本点
plt.scatter(x_test[:, 0], x_test[:, 1], s=200, facecolor='yellow', zorder=10, marker='+') # 测试点
#给测试点加上黄十字,予以辨别
plt.xlabel(iris_feature[0], fontsize=20)
plt.ylabel(iris_feature[1], fontsize=20)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title('svm in iris data classification', fontsize=30)
plt.grid()
plt.show()
结果如下:
高斯核:
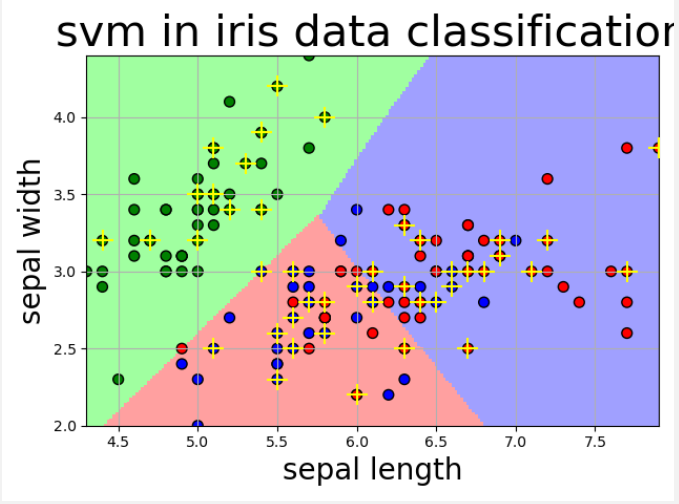
线性核:
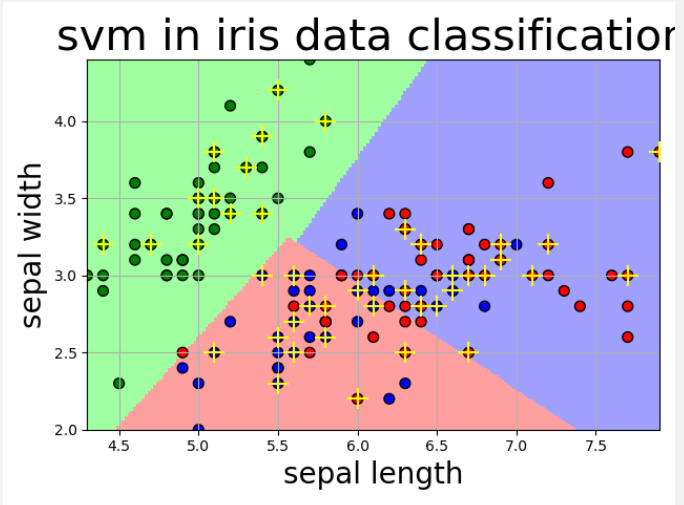
五、实验心得
- 支持向量机的关键技术:支持向量机性能的优劣主要取决于核函数的选取,所以对于一个实际问题而言,如何根据实际的数据模型选择合适的核函数从而构造 $SVM$ 算法.目前比较成熟的核函数及其参数的选择都是人为的,根据经验来选取的,带有一定的随意性.在不同的问题领域,核函数应当具有不同的形式和参数,所以在选取时候应该将领域知识引入进来.
- 在进行分类训练时,也要注意正负样本的均衡问题,我们可以采用上面提到的一些方法进行解决。
- 在接下来需要尝试将不同的训练样本训练出模型,调整正负样本的比例,寻找最优参数的设置,提高模型的分类预测正确率。
