数据挖掘实验
一、实验目的
掌握Apriori算法的原理。
二、实验要求
- 理解频繁项集和关联规则。
- 熟练使用Python或其他工具实现Apriori算法。
三、实验器材
- 计算机一台。
- Python或其他编程工具。
四、实验内容
Apriori 算法
基本概念
-
项与项集:设 $itemset={item1, item_2, …, item_m}$ 是所有项的集合,其中,$item_k(k=1,2,…,m)$ 成为项。项的集合称为项集($itemset$),包含k个项的项集称为k项集($k-itemset$)。
-
事务与事务集:一个事务T是一个项集,它是 $itemset$ 的一个子集,每个事务均与一个唯一标识符 $T_{id}$ 相联系。不同的事务一起组成了事务集D,它构成了关联规则发现的事务数据库。
-
关联规则:关联规则是形如A=>B的蕴涵式,其中 $A、B$ 均为 $itemset$ 的子集且均不为空集,而 $A$ 交 $B$ 为空。
-
支持度(support):关联规则的支持度定义如下: \(support(A=>B) = P(A ∪B)\) 其中 $P(A ∪B)$ 表示事务包含集合 $A$ 和 $B$ 的并(即包含A和B中的每个项)的概率。注意与 $P(A or B)$ 区别,后者表示事务包含 $A$ 或 $B$ 的概率。
-
置信度(confidence):关联规则的置信度定义如下:
- 项集的出现频度(support count):包含项集的事务数,简称为项集的频度、支持度计数或计数。
- 频繁项集(frequent itemset):如果项集I的相对支持度满足事先定义好的最小支持度阈值(即I的出现频度大于相应的最小出现频度(支持度计数)阈值),则 $I$ 是频繁项集。
- 强关联规则:满足最小支持度和最小置信度的关联规则,即待挖掘的关联规则。
频繁项集的评估标准
常用的频繁项集的评估标准有三个,分别是支持度、置信度和提升度。
支持度就是几个关联的数据在数据集出现的次数占总数据集的比重,或者说几个数据关联出现的概率。如果我们有两个想分析关联性的数据 X 和 Y,则对应的支持度为: \(Support(X,Y)=P(XY)=\frac{number(XY)}{num(AllSamples)}\) 以此类推,如果我们有三个想分析关联性的数据 X 、 Y 和 Z,则对应的支持度为: \(Support(X,Y,Z)=P(XYZ)=\frac{number(XYZ)}{num(AllSamples)}\) 一般来说,支持度高的数据不一定构成频繁项集,但支持度太低的数据肯定无法构成频繁项集。
置信度体现了一个数据出现之后,另一个数据出现的概率。或者可以称为数据的条件概率。
如果我们有两个想要分析关联性的数据 X 和 Y,X 对 Y 的置信度为: \(Confidence(X⇐Y)=P(X|Y)=P(XY)/P(Y)\) 也可以以此类推到多个数据的关联置信度, 比如对于三个数据 X、Y、 Z,则 X 对于 Y 和 Z 的置信度为: \(Confidence(X⇐YZ)=P(X|YZ)=P(XYZ)/P(YZ)\)
提升度表示含有 Y 的条件下, 同时含有 X 的概率与 X 总体发生的概率之比, 即: \(Lift(X⇐Y)=P(X|Y)/P(X)=Confidence(X⇐Y)/P(X)\) 提升度体现了 $X$ 和 $Y$ 之间的关联关系,提升度大于1则 $X⇐YX⇐Y$ 是有效的强关联规则, 提升度小于等于1则 $X⇐YX⇐Y$ 是无效的强关联规则 。一个特殊的情况,如果$X$ 和 $Y$ 独立,则有 $Lift(X⇐Y)=Lift(X⇐Y)=1$,因为此时$P(X|Y)=P(X)P(X|Y)=P(X)$。
一般来说,要选择一个数据集合中的频繁项集,则需要自己定义评估标准。最常用的评估标准是用自定义的支持度,或者是自定义支持度和置信度的一个组合。
算法思想
对于 $Apriori$ 算法,我们使用支持度来作为我们判断频繁项集的标准。$Apriori$ 算法的目标是找到最大的 $K$ 项频繁集。这里有两层意思,首先,我们要找到符合支持度标准的频繁集。但是这样的频繁集可能有很多。第二层意思就是我们要找到最大个数的频繁集。比如我们找到符合支持度的频繁集$AB$ 和 $ABE$,那么我们会抛弃 $AB$,只保留 $ABE$,因为 $AB$ 是2项频繁集,而ABE是3项频繁集。那么具体的,$Apriori$ 算法是如何做到挖掘K项频繁集的呢?
$Aprior$ 算法采用了迭代的方法,先搜索出候选1项集及对应的支持度,剪枝去掉低于支持度的1项集,得到频繁1项集。然后对剩下的频繁1项集进行连接,得到候选的频繁2项集,筛选去掉低于支持度的候选频繁2项集,得到真正的频繁二项集,以此类推,迭代下去,直到无法找到频繁 $k+1$ 项集为止,对应的频繁k项集的集合即为算法的输出结果。
第一步通过迭代,检索出事务数据库中的所有频繁项集,即支持度不低于用户设定的阈值的项集;
第二步利用频繁项集构造出满足用户最小信任度的规则。
具体做法就是:
首先找出频繁1-项集,记为L1;然后利用L1来产生候选项集C2,对C2中的项进行判定挖掘出L2,即频繁2-项集;不断如此循环下去直到无法发现更多的频繁k-项集为止。每挖掘一层Lk就需要扫描整个数据库一遍。算法利用了一个性质:
Apriori 性质:任一频繁项集的所有非空子集也必须是频繁的。意思就是说,生成一个 $k-itemset$ 的候选项时,如果这个候选项有子集不在$(k-1)-itemset$(已经确定是frequent的)中时,那么这个候选项就不用拿去和支持度判断了,直接删除。具体而言:
1) 连接步
为找出$L_k$ (所有的频繁k项集的集合),通过将$L_{k-1}$(所有的频繁k-1项集的集合)与自身连接产生候选k项集的集合。候选集合记作$C_k$。设$l1$ 和$l2$ 是$L_{k-1}$ 中的成员。记$li[j]$ 表示$li$中的第j项。假设$Apriori$ 算法对事务或项集中的项按字典次序排序,即对于$(k-1)$ 项集$li$ ,$li[1]i</sub>[2]<……….i</sub>[k-1]$。将$L_{k-1}$与自身连接,如果 (l1[1]=l2[1])&&( l1[2]=l2[2])&&……..&& (l1[k-2]=l2[k-2])&&(l1[k-1]2</sub>[k-1]),那认为 $l1$ 和 $l2$ 是可连接。连接l1和 $l2$ 产生的结果是 ${l1[1],l1[2],……,l1[k-1],l2[k-1]}$。2) 剪枝步
$C_K$是 $L_K$的超集,也就是说,$C_K$ 的成员可能是也可能不是频繁的。通过扫描所有的事务(交易),确定 $C_K$ 中每个候选的计数,判断是否小于最小支持度计数,如果不是,则认为该候选是频繁的。为了压缩 $C_k$ ,可以利用 $Apriori$ 性质:任一频繁项集的所有非空子集也必须是频繁的,反之,如果某个候选的非空子集不是频繁的,那么该候选肯定不是频繁的,从而可以将其从 $CK$ 中删除。
算法流程
下面我们对 $Aprior$ 算法流程做一个总结。
输入:数据集合 $D$,支持度阈值 $α$
输出:最大的频繁k项集
1. 扫描整个数据集,得到所有出现过的数据,作为候选频繁1项集。$k=1$,频繁0项集为空集。
2. 挖掘频繁 $k$ 项集
a) 扫描数据计算候选频繁 $k$ 项集的支持度
b) 去除候选频繁k项集中支持度低于阈值的数据集,得到频繁k项集。如果得到的频繁k项集为空,则直接返回频繁k-1项集的集合作为算法结果,算法结束。如果得到的频繁k项集只有一项,则直接返回频繁k项集的集合作为算法结果,算法结束。
c) 基于频繁k项集,连接生成候选频繁 $k+1$ 项集。
3. 令 $k=k+1$,转入步骤2。
从算法的步骤可以看出,$Aprior$ 算法每轮迭代都要扫描数据集,因此在数据集很大,数据种类很多的时候,算法效率很低。
示例图如下:
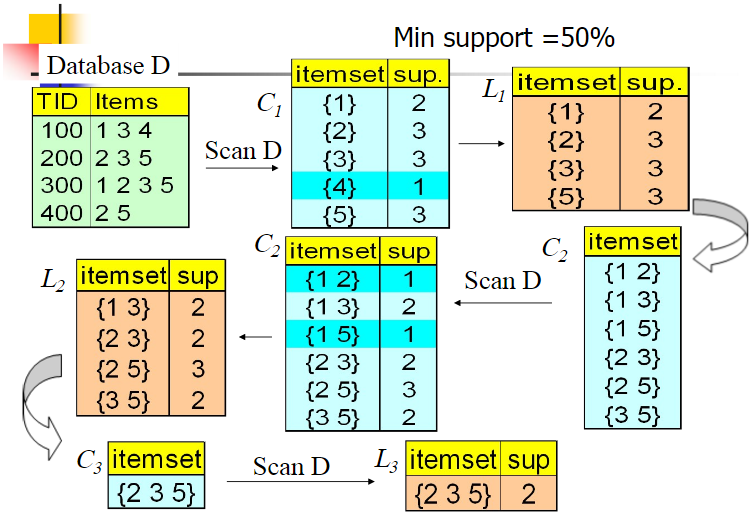
算法的改进方法
方法1:基于hash表的项集计数
将每个项集通过相应的hash函数映射到hash表中的不同的桶中,这样可以通过将桶中的项集技术跟最小支持计数相比较先淘汰一部分项集。
方法2:事务压缩(压缩进一步迭代的事务数)
不包含任何k-项集的事务不可能包含任何(k+1)-项集,这种事务在下一步的计算中可以加上标记或删除。
方法3:划分
挖掘频繁项集只需要两次数据扫描。
D中的任何频繁项集必须作为局部频繁项集至少出现在一个部分中。
第一次扫描:将数据划分为多个部分并找到局部频繁项集。
第二次扫描:评估每个候选项集的实际支持度,以确定全局频繁项集。
方法4:选样(在给定数据的一个子集挖掘)
基本思想:选择原始数据的一个样本,在这个样本上用 $Apriori$ 算法挖掘频繁模式。
通过牺牲精确度来减少算法开销,为了提高效率,样本大小应该以可以放在内存中为宜,可以适当降低最小支持度来减少遗漏的频繁模式。
可以通过一次全局扫描来验证从样本中发现的模式。
可以通过第二此全局扫描来找到遗漏的模式。
方法5:动态项集计数
在扫描的不同点添加候选项集,这样,如果一个候选项集已经满足最少支持度,则在可以直接将它添加到频繁项集,而不必在这次扫描的以后对比中继续计算。
算法优化思路
1、在逐层搜索循环过程的第 $k$ 步中,根据 $k-1$ 步生成的 $k-1$ 维频繁项目集来产生k维候选项目集,由于在产生 $k-1$ 维频繁项目集时,我们可以实现对该集中出现元素的个数进行计数处理,因此对某元素而言,若它的计数个数不到 $k-1$ 的话,可以事先删除该元素,从而排除由该元素将引起的大规格所有组合。
这是因为对某一个元素要成为 $K$ 维项目集的一元素的话,该元素在 $k-1$ 阶频繁项目集中的计数次数必须达到 $K-1$ 个,否则不可能生成K维项目集(性质3)。
2、根据以上思路得到了这个候选项目集后,可以对数据库 $D$ 的每一个事务进行扫描,若该事务中至少含有候选项目集 $C_k$ 中的一员则保留该项事务,否则把该事物记录与数据库末端没有作删除标记的事务记录对换,并对移到数据库末端的事务记录作删除标一记,整个数据库扫描完毕后为新的事务数据库 $ D’ $ 中。
因此随着 $K$ 的增大,$D’$ 中事务记录量大大地减少,对于下一次事务扫描可以大大节约 I/0 开销。由于顾客一般可能一次只购买几件商品,因此这种虚拟删除的方法可以实现大量的交易记录在以后的挖掘中被剔除出来,在所剩余的不多的记录中再作更高维的数据挖掘是可以大大地节约时间的。
当然还有很多相应的优化算法,比如针对 $Apriori$ 算法的性能瓶颈问题-需要产生大量候选项集和需要重复地扫描数据库,2000年 Jiawei Han 等人提出了基于 $FP$ 树生成频繁项集的 $FP-growth$ 算法。该算法只进行2次数据库扫描且它不使用侯选集,直接压缩数据库成一个频繁模式树,最后通过这棵树生成关联规则。研究表明它比 $Apriori$ 算法大约快一个数量级。
生成频繁项集代码
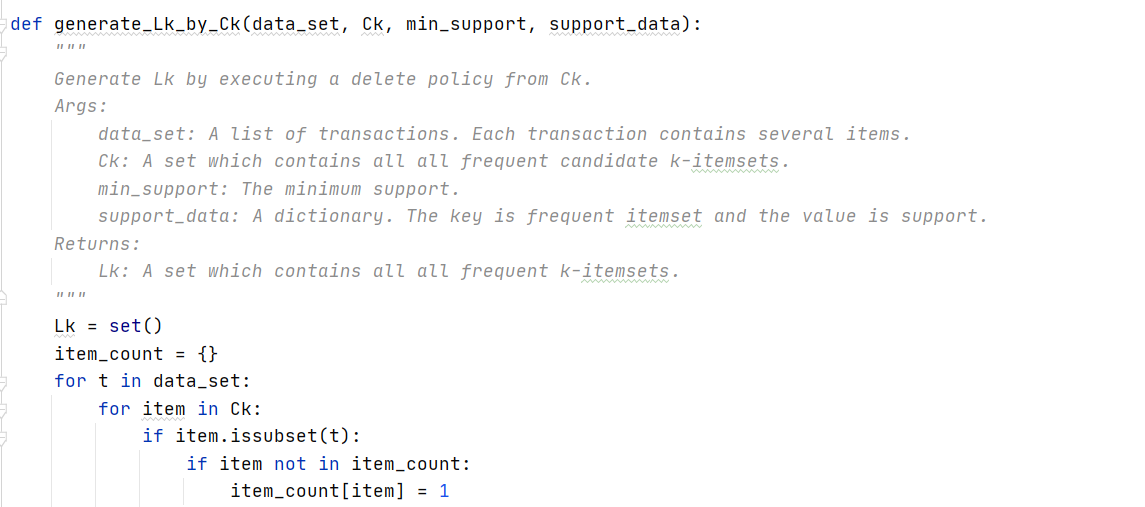

输入数据集

输入最小支持度阈值

输出频繁项集结果
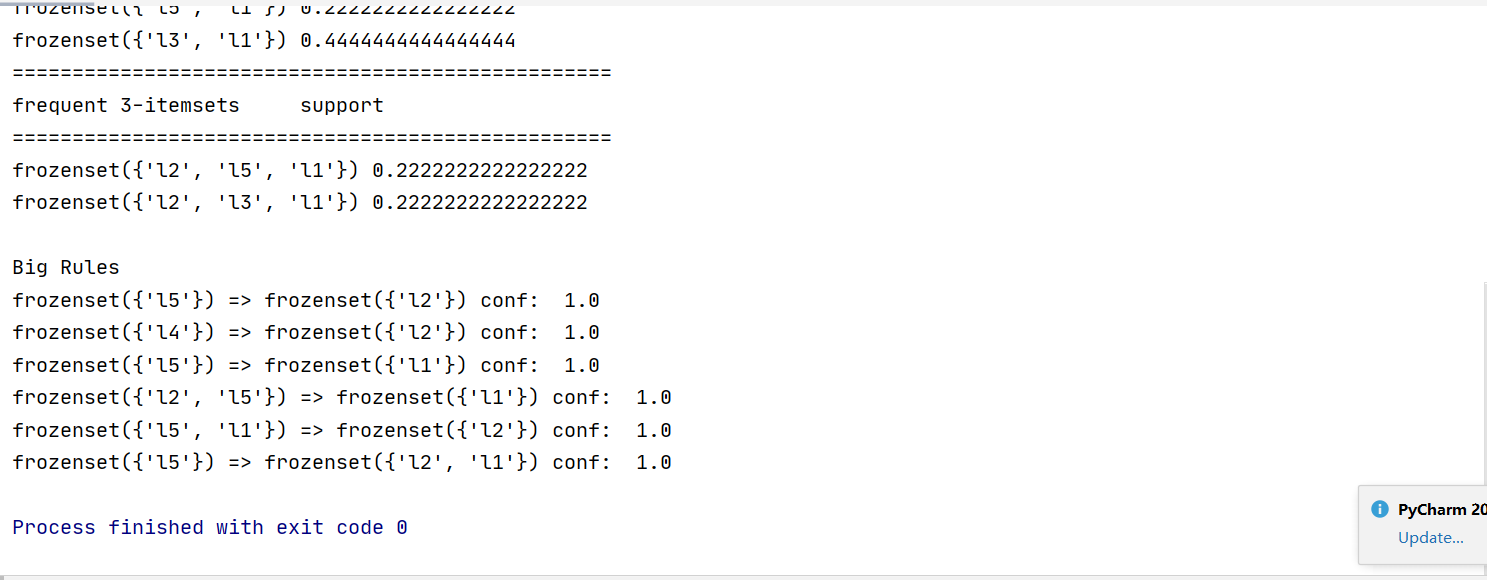
五、实验心得
通过这次实验, 我学会了如何使用 $Apriori$ 算法, 并且对支持度、 置信度等概念有了一个更加深入的了解,收获颇丰。
