数据挖掘实验
一、实验目的
掌握PCA算法的原理
二、实验要求
- 理解数据降维过程
- 熟练使用Python或其他工具实现PCA算法
三、实验器材
- 计算机一台
- Python或其他编程工具
四、实验内容
PCA原理详解
PCA的概念
PCA (Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法。PCA 的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
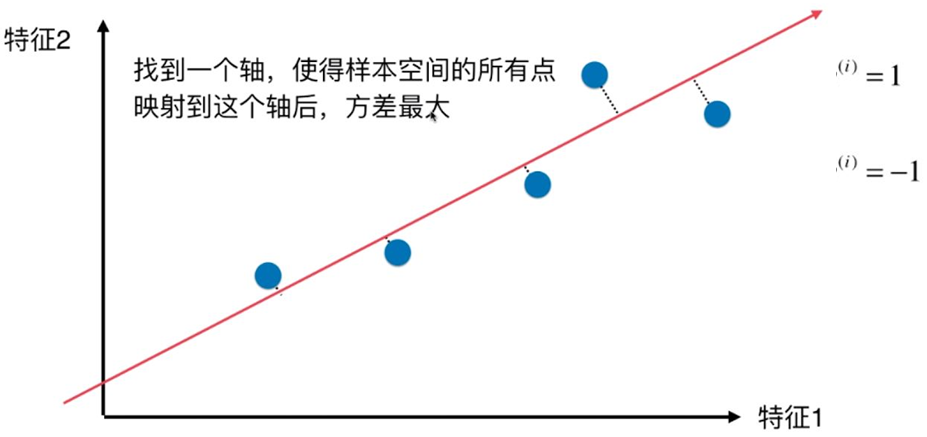
PCA 的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推,可以得到 n 个这样的坐标轴。通过这种方式获得的新的坐标轴,我们发现,大部分方差都包含在前面 k 个坐标轴中,后面的坐标轴所含的方差几乎为0。
于是,我们可以忽略余下的坐标轴,只保留前面k个含有绝大部分方差的坐标轴。事实上,这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,实现对数据特征的降维处理。
PCA本质上是将方差最大的方向作为主要特征,并且在各个正交方向上将数据“离相关”,也就是让它们在不同正交方向上没有相关性。
协方差矩阵和散度矩阵
样本的均值: \(\overline{x} = \frac{1}{n}\sum_{i = 1}^{N} \overline{x}\) 样本方差: \(S ^2 = \frac{1}{n - 1}\sum_{i = 1}^{n}(x_i - \overline{x})^2\) 样本 X 和样本 Y 的协方差: \(Cov(X, Y) = E[(X - E(X))(Y - E(Y))] = \frac{1}{n - 1}\sum_{i = 1}^{n} (x_i - \overline{x})(y_i - \overline{y})\) 由上面的公式,我们可以得到以下结论:
-
方差的计算公式是针对一维特征,即针对同一特征不同样本的取值来进行计算得到;而协方差则必须要求至少满足二维特征;方差是协方差的特殊情况。
-
方差和协方差的除数是 n-1 ,这是为了得到方差和协方差的无偏估计。
协方差为正时,说明X和Y是正相关关系;协方差为负时,说明 $X$ 和 $Y$ 是负相关关系;协方差为0时,说明X和Y是相互独立。 $Cov(X,X) $就是 $X$ 的方差。当样本是n维数据时,它们的协方差实际上是协方差矩阵(对称方阵)。
特征值分解矩阵原理
特征值与特征向量
如果一个向量 v 是矩阵 A 的特征向量,将一定可以表示成下面的形式: \(Av = λv\) 其中,λ是特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。
特征值分解矩阵
对于矩阵A,有一组特征向量v,将这组向量进行正交化单位化,就能得到一组正交单位向量。特征值分解,就是将矩阵A分解为如下式: \(A = Q\sum{}Q^{-1}\) 其中, $Q$ 是矩阵 $A$ 的特征向量组成的矩阵,$\sum$ 则是一个对角阵,对角线上的元素就是特征值。
基于特征值分解协方差矩阵实现 PCA 算法
输入:数据集$X = \left{x_1, x_2, x_3, …, x_n\right}$ ,需要降到 $k$ 维。
- 去平均值(即去中心化),即每一位特征减去各自的平均值。
- 计算协方差矩阵 $\frac{1}{n} {X}X^T$,注:这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。
- 用特征值分解方法求协方差矩阵$\frac{1}{n} {X}X^T$ 的特征值与特征向量。
- 对特征值从大到小排序,选择其中最大的 $k$ 个。然后将其对应的 $k$ 个特征向量分别作为行向量组成特征向量矩阵P。
- 将数据转换到k个特征向量构建的新空间中,即 $Y=PX$。
PCA算法优点
- 使得数据集更易使用。
- 降低算法的计算开销。
- 去除噪声。
- 使得结果容易理解。
- 完全无参数限制。
PCA算法缺点
- 如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高;
- 特征值分解有一些局限性,比如变换的矩阵必须是方阵;
- 在非高斯分布情况下,PCA方法得出的主元可能并不是最优的。
PCA算法应用
- 高维数据集的探索与可视化。
- 数据压缩。
- 数据预处理。
- 图象、语音、通信的分析处理。
- 降维(最主要),去除数据冗余与噪声。
代码部分
数据标准化(去均值)代码
def nomalization(X):
#对数据进行标准化
global feature_nums
sample_nums, feature_nums = X.shape # N x M
arr_mean = [np.mean(X[:, i]) for i in range(0, feature_nums, 1)]
arr_normalization = X - arr_mean #broadcast(可能
#print("标准化矩阵:", arr_normalization)
return arr_normalization
求协方差矩阵代码
def get_convariance_matrix(X):
#求解 协方差矩阵
#np.transpose 求转置矩阵
transpose_X = np.transpose(X)
convariance_matrix = np.dot(transpose_X, X ) #注意前后顺序!!!!!
print("协方差矩阵:", convariance_matrix)
return convariance_matrix
求特征值和特征向量代码
def get_eigenvalues_and_eigenvacors(X, k):
#获取 协方差矩阵的 特征值 和 特征向量
#print(np.shape(X))
eigenvalues, eigenvactors = np.linalg.eig(X)
print("特征值:",eigenvalues)
print()
print("特征向量:",eigenvactors)
print()
eigen_couples = [(eigenvalues[i], eigenvactors[:, i]) for i in range(0, feature_nums, 1)] ##
eigen_couples.sort(reverse = True)
feature_arr = np.array([val[1] for val in eigen_couples[:k]])
print("向量数组:",feature_arr)
return feature_arr
其他代码
def PCa(X, K):
#进行PCA 操作
arr_normalization = nomalization(X)
convariance_matrix = get_convariance_matrix(arr_normalization)
feature_arr = get_eigenvalues_and_eigenvacors(convariance_matrix, K)
result = np.dot( arr_normalization, np.transpose(feature_arr) )
return result
pass
if __name__ == "__main__":
iris = datasets.load_iris() #直接获取 iris 数据集
#print(iris)
data = iris["data"]
feature = iris["feature_names"]
result = PCa(data, 2)
#print(result)
x1 = [result[i][0] for i in range(0, 50, 1)]
x2 = [result[i][0] for i in range(50, 100, 1)]
x3 = [result[i][0] for i in range(100, 150, 1)]
y1 = [result[i][1] for i in range(0, 50, 1)]
y2 = [result[i][1] for i in range(50, 100, 1)]
y3 = [result[i][1] for i in range(100, 150, 1)]
plt.plot(x1, y1, "o", color = "red")
plt.plot(x2, y2, "o", color = "blue")
plt.plot(x3, y3, "o", color = "green")
plt.xlabel("X")
plt.ylabel("Y")
plt.title("PCA result")
plt.show()
#pca = PCA(n_components = 2)
#pca.fit(data)
#print(np.shape(pca.transform(data)))
实验结果
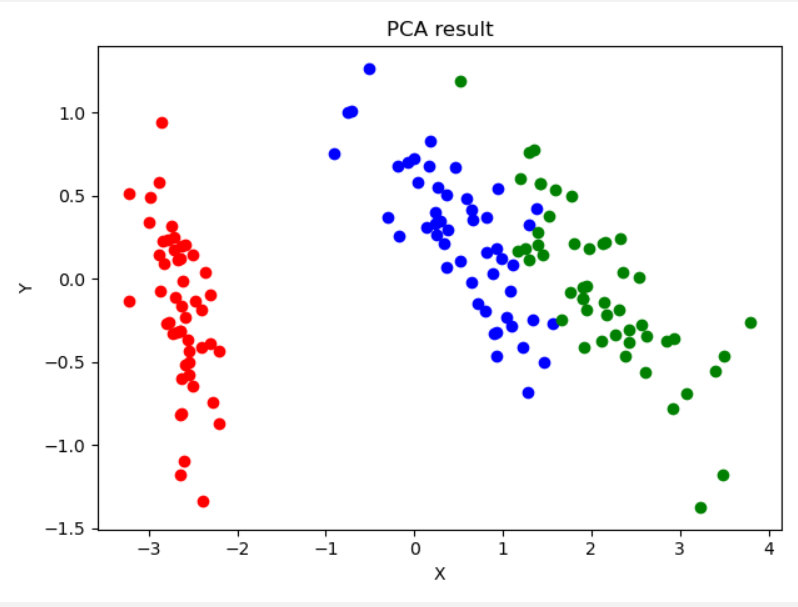
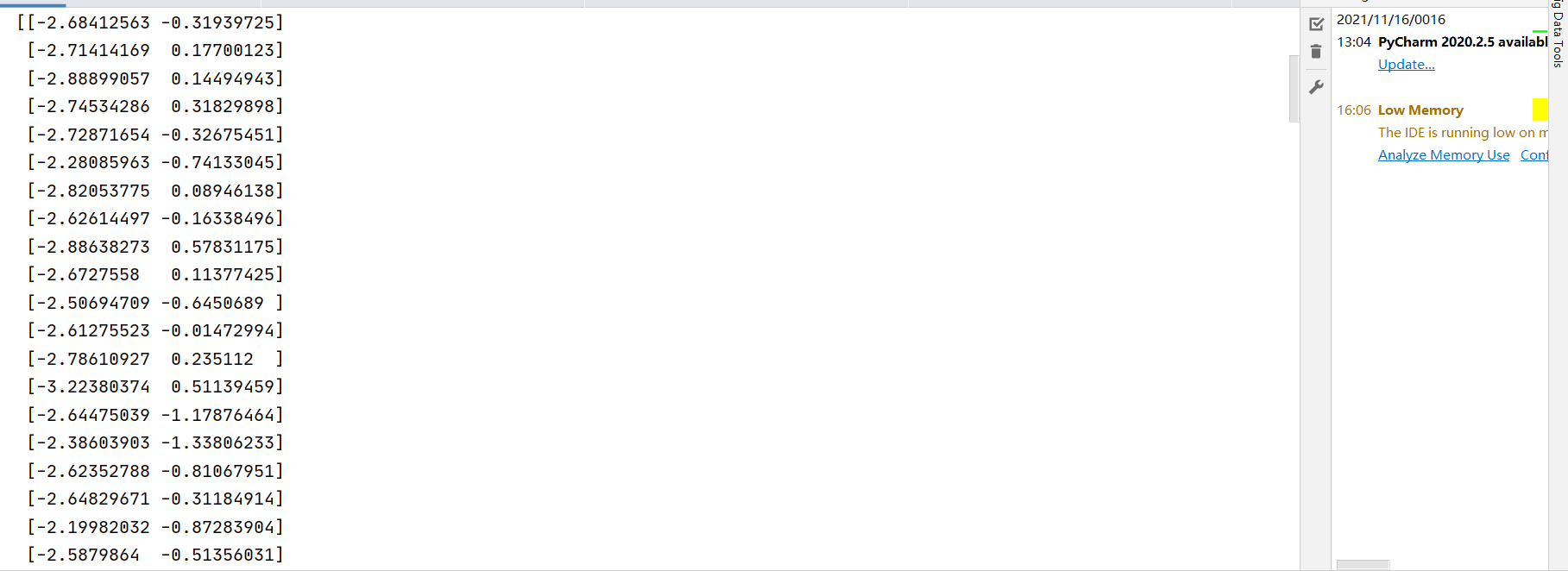
五、实验心得
通过这次实验, 我学会了如何使用PCA算法来对数据进行降维处理,并且对numpy、 pyplot 等库有了一个更加深入的了解。
