通过遗传算法解决数学问题
实验内容
用遗传算法求解例2的优化问题。设计 种群大小、染色体长度、交叉变异概率等。
实验原理
遗传算法
科学定义
遗传算法$(Genetic\ Algorithm,\ GA)$是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,不需要确定的规则就能自动获取和指导优化的搜索空间,自适应地调整搜索方向。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
执行过程
遗传算法是从代表问题可能潜在的解集的一个种群$(population)$开始的,而一个种群则由经过基因$(gene)$编码的一定数目的个体 $(individual)$ 组成。每个个体实际上是染色体 $(chromosome)$ 带有特征的实体。
染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现,如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此,在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码。
初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代$(generation)$演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度$(fitness)$大小选择$(selection)$个体,并借助于自然遗传学的遗传算子$(genetic operators)$进行组合交叉$(crossover)$和变异$(mutation)$,产生出代表新的解集的种群。
这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码$(decoding)$,可以作为问题近似最优解。
过程图解
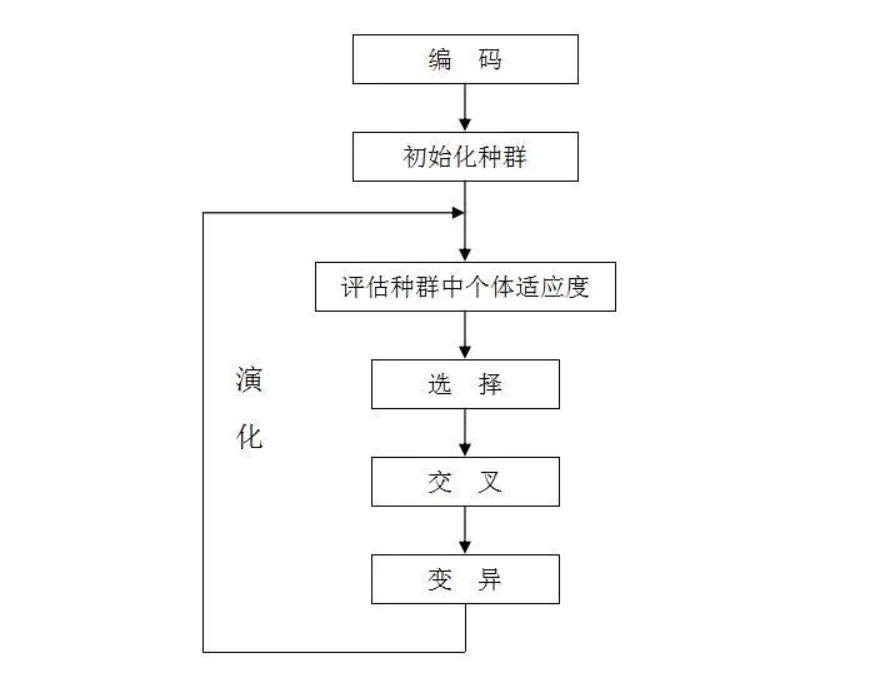
相关术语
-
基因型 $(genotype)$:性状染色体的内部表现;
-
表现型 $(phenotype)$:染色体决定的性状的外部表现,或者说,根据基因型形成的个体的外部表现;
-
进化 $(evolution)$:种群逐渐适应生存环境,品质不断得到改良。生物的进化是以种群的形式进行的。
-
适应度 $(fitness)$:度量某个物种对于生存环境的适应程度。
-
选择 $(selection)$:以一定的概率从种群中选择若干个个体。一般,选择过程是一种基于适应度的优胜劣汰的过程。
-
复制 $(reproduction)$:细胞分裂时,遗传物质 $DNA$ 通过复制而转移到新产生的细胞中,新细胞就继承了旧细胞的基因。
-
交叉 $(crossover)$:两个染色体的某一相同位置处 $DNA$ 被切断,前后两串分别交叉组合形成两个新的染色体。也称基因重组或杂交;
-
变异 $(mutation)$:复制时可能(很小的概率)产生某些复制差错,变异产生新的染色体,表现出新的性状。
-
编码 $(coding)$:$DNA$ 中遗传信息在一个长链上按一定的模式排列。遗传编码可看作从表现型到基因型的映射。
-
解码 $(decoding)$:基因型到表现型的映射。
-
个体 $(individual)$:指染色体带有特征的实体;
-
种群 $(population)$:个体的集合,该集合内个体数称为种群
二进制编码法
就像人类的基因有 $AGCT\ 4$ 种碱基序列一样。不过在这里我们只用了 $0$ 和 $1$ 两种碱基,然后将他们串成一条链形成染色体。一个位能表示出 $2$ 种状态的信息量,因此足够长的二进制染色体便能表示所有的特征。这便是二进制编码。如下: $1110001010111$
它由二进制符号 $0$ 和 $1$ 所组成的二值符号集。它有以下一些优点:
- 编码、解码操作简单易行
- 交叉、变异等遗传操作便于实现
- 合最小字符集编码原则
- 利用模式定理对算法进行理论分析。
二进制编码的缺点是:对于一些连续函数的优化问题,由于其随机性使得其局部搜索能力较差,如对于一些高精度的问题(如上题),当解迫近于最优解后,由于其变异后表现型变化很大,不连续,所以会远离最优解,达不到稳定。
浮点编码法
二进制编码虽然简单直观,但明显地。但是存在着连续函数离散化时的映射误差。个体长度较短时,可能达不到精度要求,而个体编码长度较长时,虽然能提高精度,但增加了解码的难度,使遗传算法的搜索空间急剧扩大。
所谓浮点法,是指个体的每个基因值用某一范围内的一个浮点数来表示。在浮点数编码方法中,必须保证基因值在给定的区间限制范围内,遗传算法中所使用的交叉、变异等遗传算子也必须保证其运算结果所产生的新个体的基因值也在这个区间限制范围内。如下所示:
$1.2-3.2-5.3-7.2-1.4-9.7$
浮点数编码方法有下面几个优点:
- 适用于在遗传算法中表示范围较大的数
- 适用于精度要求较高的遗传算法
- 便于较大空间的遗传搜索
- 改善了遗传算法的计算复杂性,提高了运算交率
- 便于遗传算法与经典优化方法的混合使用
- 便于设计针对问题的专门知识的知识型遗传算子
- 便于处理复杂的决策变量约束条件
符号编码法
符号编码法是指个体染色体编码串中的基因值取自一个无数值含义、而只有代码含义的符号集如{A,B,C…}。 符号编码的主要优点是:
- 符合有意义积术块编码原则
- 便于在遗传算法中利用所求解问题的专门知识
- 便于遗传算法与相关近似算法之间的混合使用。
适应度函数
适应度函数主要是通过个体特征从而判断个体的适应度。
适应度函数也称评价函数,是根据目标函数确定的用于区分群体中个体好坏的标准。适应度函数总是非负的,而目标函数可能有正有负,故需要在目标函数与适应度函数之间进行变换。
评价个体适应度的一般过程为:
- 对个体编码串进行解码处理后,可得到个体的表现型。
- 由个体的表现型可计算出对应个体的目标函数值。
- 根据最优化问题的类型,由目标函数值按一定的转换规则求出个体的适应度。
选择函数
遗传算法中的选择操作就是用来确定如何从父代群体中按某种方法选取那些个体,以便遗传到下一代群体。选择操作用来确定重组或交叉个体,以及被选个体将产生多少个子代个体。
那么,怎么建立这种概率关系呢?
下面介绍几种常用的选择算子:
-
轮盘赌选择(Roulette Wheel Selection):是一种回放式随机采样方法。每个个体进入下一代的概率等于它的适应度值与整个种群中个体适应度值和的比例。选择误差较大。
-
随机竞争选择(Stochastic Tournament):每次按轮盘赌选择一对个体,然后让这两个个体进行竞争,适应度高的被选中,如此反复,直到选满为止。
-
最佳保留选择:首先按轮盘赌选择方法执行遗传算法的选择操作,然后将当前群体中适应度最高的个体结构完整地复制到下一代群体中。
-
无回放随机选择(也叫期望值选择Excepted Value Selection):根据每个个体在下一代群体中的生存期望来进行随机选择运算。方法如下:
(1) 计算群体中每个个体在下一代群体中的生存期望数目N。
(2) 若某一个体被选中参与交叉运算,则它在下一代中的生存期望数目减去 $0.5$,若某一个体未 被选中参与交叉运算,则它在下一代中的生存期望数目减去 $1.0$。
(3) 随着选择过程的进行,若某一个体的生存期望数目小于0时,则该个体就不再有机会被选中。
-
确定式选择:按照一种确定的方式来进行选择操作。具体操作过程如下:
(1) 计算群体中各个个体在下一代群体中的期望生存数目 $N$。
(2) 用N的整数部分确定各个对应个体在下一代群体中的生存数目。
(3) 用 $N$ 的小数部分对个体进行降序排列,顺序取前 $M$ 个个体加入到下一代群体中。至此可完全确定出下一代群体中 $M$ 个个体。
-
无回放余数随机选择:可确保适应度比平均适应度大的一些个体能够被遗传到下一代群体中,因而选择误差比较小。
-
均匀排序:对群体中的所有个体按期适应度大小进行排序,基于这个排序来分配各个个体被选中的概率。
-
最佳保存策略:当前群体中适应度最高的个体不参与交叉运算和变异运算,而是用它来代替掉本代群体中经过交叉、变异等操作后所产生的适应度最低的个体。
-
随机联赛选择:每次选取几个个体中适应度最高的一个个体遗传到下一代群体中。
-
排挤选择:新生成的子代将代替或排挤相似的旧父代个体,提高群体的多样性。
染色体交叉
遗传算法的交叉操作,是指对两个相互配对的染色体按某种方式相互交换其部分基因,从而形成两个新的个体。
适用于二进制编码个体或浮点数编码个体的交叉算子:
-
单点交叉$(One-point Crossover)$:指在个体编码串中只随机设置一个交叉点,然后再该点相互交换两个配对个体的部分染色体。
-
两点交叉与多点交叉:
(1) 两点交叉$(Two-point Crossover)$:在个体编码串中随机设置了两个交叉点,然后再进行部分基因交换。
(2) 多点交叉$(Multi-point Crossover)$
-
均匀交叉(也称一致交叉,$Uniform Crossover$):两个配对个体的每个基因座上的基因都以相同的交叉概率进行交换,从而形成两个新个体。
-
算术交叉$(Arithmetic Crossover)$:由两个个体的线性组合而产生出两个新的个体。该操作对象一般是由浮点数编码表示的个体。
咳咳,根据国际惯例。还是抓一个最简单的二进制单点交叉为例来给大家讲解讲解。
二进制编码的染色体交叉过程非常类似高中生物中所讲的同源染色体的联会过程――随机把其中几个位于同一位置的编码进行交换,产生新的个体。
基因突变
遗传算法中的变异运算,是指将个体染色体编码串中的某些基因座上的基因值用该基因座上的其它等位基因来替换,从而形成新的个体。
例如下面这串二进制编码:
$101101001011001$
经过基因突变后,可能变成以下这串新的编码:
001101011011001
以下变异算子适用于二进制编码和浮点数编码的个体:
- 基本位变异$(Simple Mutation)$:对个体编码串中以变异概率、随机指定的某一位或某几位仅因座上的值做变异运算。
- 均匀变异$(Uniform Mutation)$:分别用符合某一范围内均匀分布的随机数,以某一较小的概率来替换个体编码串中各个基因座上的原有基因值。(特别适用于在算法的初级运行阶段)
- 边界变异$(Boundary Mutation)$:随机的取基因座上的两个对应边界基因值之一去替代原有基因值。特别适用于最优点位于或接近于可行解的边界时的一类问题。
- 非均匀变异:对原有的基因值做一随机扰动,以扰动后的结果作为变异后的新基因值。对每个基因座都以相同的概率进行变异运算之后,相当于整个解向量在解空间中作了一次轻微的变动。
- 高斯近似变异:进行变异操作时用符号均值为P的平均值,方差为P**2的正态分布的一个随机数来替换原有的基因值。
实验代码
进行一些变量的初始化。
DNA_SIZE = 17 #染色体长度
POPULATION_SIZE = 8 #种群大小
ITERATIONS_SIZE = 30 #整个种群迭代次数
X1_BOUND = [-5, 5] #x1的取值范围
X2_BOUND = [-5, 5] #x2的取值范围
CROSS_OVER_RATE = 0.7 #交叉的概率
SINGLE_MUTATIONS_RATE = 0.1 #单点变异的概率
函数用于将二进制转换为十进制的数。
def encoding(bin):
#编码, 二进制 -----> 十进制的数~
return int(bin, 2)
pass
由实际目标而定,在本次实验中为将十进制的数映射在 $[-5, 5]$ 的范围内。
def decoding(x):
#解码, 十进制 -----> 映射在[-5, 5]的范围中
temp_x = X1_BOUND[0] + x * (X1_BOUND[1] - X1_BOUND[0]) / (2 ** DNA_SIZE - 1)
return temp_x
pass
单点交叉,当满足所给定的概率后,对染色体中随机的一位进行单点交叉。
def single_cross_over(x1, x2):
#单点交叉感染
probability = random.random()
if probability <= CROSS_OVER_RATE:
#发生交叉
occur_position = random.randint(0, 13)
arr_1 = list(x1)
arr_2 = list(x2)
temp = arr_1[occur_position]
arr_1[occur_position] = arr_2[occur_position]
arr_2[occur_position] = temp
x1 = "".join(arr_1)
x2 = "".join(arr_2)
pass
else:
#不发生交叉
pass
return x1, x2
轮盘赌选择,在后面的实验中会给出更加简便的写法。
def roulette(arr):
#轮盘赌选择 arr 应为二进制
number = [] #实际的数字的 列表
for i in range(0, len(arr), 1):
number.append(decoding(encoding(arr[i])))
fitness_arr = [] #适应值列表
x1_arr = number[0::2] #x1取偶数位
x2_arr = number[1: : 2] #x1取奇数位
length = len(x1_arr)
for i in range(0, length, 1):
fitness = eval(x1_arr[i], x2_arr[i])
fitness_arr.append(fitness)
#fitness_arr = generate_fitness_arr(arr)
Probability = []
total_sum = sum(fitness_arr)
for i in range(0, length, 1):
Probability.append(fitness_arr[i] / total_sum) #每一队的概率
for i in range(1, length, 1):
Probability[i] += Probability[i - 1] #轮盘赌叠加
#Probability.sort()
#Probability = sorted(Probability)
#random_number = random.random() #生成0 - 1 之间
result = []
print("概率数组是:", Probability)
for i in range(0, length, 1):
random_number = random.random() # 生成0 - 1 之间
print("随机数是:", random_number)
temp = 0 #注意放的位置
for j in range(0, length, 1):
# if random_number >= temp and random_number <= Probability[j]:
# result.append(arr[j]) # x1
# result.append(arr[j + 1]) # x2
# temp = Probability[j]
# break
if j == 0 and random_number <= Probability[j]:
result.append(arr[j])
result.append(arr[j + 1])
break
#j > 0 and j < length - 1 and
elif random_number >=Probability[j - 1] and random_number <= Probability[j]:
result.append(arr[j])
result.append(arr[j + 1])
break
return result
单点变异。在一定的概率下,会在染色体上的随机一位发生变异。即0 ->1,1 ->0。
def single_mutations(x): #单点突变
#x:个体的二进制编码
probability = random.random() #生成 0-1之间的浮点数,与设定的概率进行比较
result = ""
if probability <= SINGLE_MUTATIONS_RATE:
# 发生变异
occur_position = random.randint(0, 13)
temp_arr = list(x)
if temp_arr[occur_position] == "1":
temp_arr[occur_position] = "0"
else:
temp_arr[occur_position] = "1"
result = "".join(temp_arr)
else:
#不发生变异
result = x
return result
评估函数,写法视具体的题目要求而定。
def eval(x1, x2):
#适应度评测函数
return 1 / (x1 ** 2 + x2 ** 2 + 1)
pass
根据给定的数目生成具有该规格个体的种群,以便后续实验的进行。
def initial_the_population(arr, num):
#种群初始化
#::num: 种群中的个体数
#arr:种群数组,将生成的个体置于数组中
for i in range(0, num, 1):
individual = generate_one_individual()
arr.append(individual)
return
一个个体的生成。
def generate_one_individual():
#产生一个个体,以二进制编码形式产生。(17位)
binary_string = []
for i in range(0, 17, 1):
temp = random.randint(0, 1)
binary_string.append(temp)
#print(binary_string)
result = "".join(str(i) for i in binary_string)
#return binary_string
return result
将二进制数转化为十进制:
def tenTotwo(number):
#定义栈
s = []
binstring = ''
flag = 0
#if number < 0:
# number = -number
# flag = 1
while number > 0:
#余数进栈
rem = number % 2
s.append(rem)
number = number // 2
while len(s) > 0:
#元素全部出栈即为所求二进制数
binstring = binstring + str(s.pop())
#print(binstring)
return binstring
完整代码如下:
# -*-coding:UTF-8 -*-
import numpy
import random
import numpy as np
import matplotlib.pyplot as plt
DNA_SIZE = 17 #染色体长度
POPULATION_SIZE = 8 #种群大小
ITERATIONS_SIZE = 30 #整个种群迭代次数
X1_BOUND = [-5, 5] #x1的取值范围
X2_BOUND = [-5, 5] #x2的取值范围
CROSS_OVER_RATE = 0.7 #交叉的概率
SINGLE_MUTATIONS_RATE = 0.1 #单点变异的概率
# class Individual:
# __slots__ = ""
def encoding(bin):
#编码, 二进制 -----> 十进制的数~
return int(bin, 2)
pass
def decoding(x):
#解码, 十进制 -----> 映射在[-5, 5]的范围中
temp_x = X1_BOUND[0] + x * (X1_BOUND[1] - X1_BOUND[0]) / (2 ** DNA_SIZE - 1)
return temp_x
pass
def single_cross_over(x1, x2):
#单点交叉感染
probability = random.random()
if probability <= CROSS_OVER_RATE:
#发生交叉
occur_position = random.randint(0, 13)
arr_1 = list(x1)
arr_2 = list(x2)
temp = arr_1[occur_position]
arr_1[occur_position] = arr_2[occur_position]
arr_2[occur_position] = temp
x1 = "".join(arr_1)
x2 = "".join(arr_2)
pass
else:
#不发生交叉
pass
return x1, x2
def roulette(arr):
#轮盘赌选择 arr 应为二进制
number = [] #实际的数字的 列表
for i in range(0, len(arr), 1):
number.append(decoding(encoding(arr[i])))
fitness_arr = [] #适应值列表
x1_arr = number[0::2] #x1取偶数位
x2_arr = number[1: : 2] #x1取奇数位
length = len(x1_arr)
for i in range(0, length, 1):
fitness = eval(x1_arr[i], x2_arr[i])
fitness_arr.append(fitness)
#fitness_arr = generate_fitness_arr(arr)
Probability = []
total_sum = sum(fitness_arr)
for i in range(0, length, 1):
Probability.append(fitness_arr[i] / total_sum) #每一队的概率
for i in range(1, length, 1):
Probability[i] += Probability[i - 1] #轮盘赌叠加
#Probability.sort()
#Probability = sorted(Probability)
#random_number = random.random() #生成0 - 1 之间
result = []
print("概率数组是:", Probability)
for i in range(0, length, 1):
random_number = random.random() # 生成0 - 1 之间
print("随机数是:", random_number)
temp = 0 #注意放的位置
for j in range(0, length, 1):
# if random_number >= temp and random_number <= Probability[j]:
# result.append(arr[j]) # x1
# result.append(arr[j + 1]) # x2
# temp = Probability[j]
# break
if j == 0 and random_number <= Probability[j]:
result.append(arr[j])
result.append(arr[j + 1])
break
#j > 0 and j < length - 1 and
elif random_number >=Probability[j - 1] and random_number <= Probability[j]:
result.append(arr[j])
result.append(arr[j + 1])
break
return result
pass
def single_mutations(x): #单点突变
#x:个体的二进制编码
probability = random.random() #生成 0-1之间的浮点数,与设定的概率进行比较
result = ""
if probability <= SINGLE_MUTATIONS_RATE:
# 发生变异
occur_position = random.randint(0, 13)
temp_arr = list(x)
if temp_arr[occur_position] == "1":
temp_arr[occur_position] = "0"
else:
temp_arr[occur_position] = "1"
result = "".join(temp_arr)
else:
#不发生变异
result = x
return result
def eval(x1, x2):
#适应度评测函数
return 1 / (x1 ** 2 + x2 ** 2 + 1)
pass
def initial_the_population(arr, num):
#种群初始化
#::num: 种群中的个体数
#arr:种群数组,将生成的个体置于数组中
for i in range(0, num, 1):
individual = generate_one_individual()
arr.append(individual)
return
def generate_one_individual():
#产生一个个体,以二进制编码形式产生。(17位)
binary_string = []
for i in range(0, 17, 1):
temp = random.randint(0, 1)
binary_string.append(temp)
#print(binary_string)
result = "".join(str(i) for i in binary_string)
#return binary_string
return result
def tenTotwo(number):
#定义栈
s = []
binstring = ''
flag = 0
#if number < 0:
# number = -number
# flag = 1
while number > 0:
#余数进栈
rem = number % 2
s.append(rem)
number = number // 2
while len(s) > 0:
#元素全部出栈即为所求二进制数
binstring = binstring + str(s.pop())
#print(binstring)
return binstring
def generate_fitness_arr(arr):
#arr 二进制的数组
number = [] # 实际的数字的 列表
for i in range(0, len(arr), 1):
number.append(decoding(encoding(arr[i])))
fitness_arr = [] # 适应值列表
x1_arr = number[0::2] # x1取偶数位
x2_arr = number[1:: 2] # x1取奇数位
length = len(x1_arr)
for i in range(0, length, 1):
fitness = eval(x1_arr[i], x2_arr[i])
fitness_arr.append(fitness)
return fitness_arr
if __name__ == "__main__":
arr_population = [] #种群数组
arr = []
initial_the_population(arr, num=POPULATION_SIZE)
#print("二进制数组是~",arr)
counts = ITERATIONS_SIZE // 10
#print("counts:", counts)
avg_fitness_arr = [] #平均符合度 数组
max_fitness_arr = [] #最大符合度 数组
for i in range(0, ITERATIONS_SIZE, 1):
#arr = [] #二进制
temp_i = i
#print(arr)
#print("长度是:", len(arr))
for i in range(0, POPULATION_SIZE, 1):
arr[i] = single_mutations(arr[i]) #单点突变
if i % 2 == 0:
arr[i], arr[i + 1] = single_cross_over(arr[i], arr[i + 1]) #交叉突变
print("变异后:")
# actual_number = []
# for i in range(0, number, 1): #实际代表的数字
# actual_number.append(decoding(encoding(arr[i])))
# #print(actual_number)
arr = roulette(arr)
actual_number = []
for i in range(0, POPULATION_SIZE, 1):
actual_number.append(decoding(encoding(arr[i])))
pass
fitness_arr = generate_fitness_arr(arr)
print("符合度数组是",fitness_arr)
# if (temp_i + 1) % counts == 0:
#
# avg_fitness_arr.append(sum(fitness_arr) / 5)
# max_fitness_arr.append(max(fitness_arr))
max_fitness_arr.append(max(fitness_arr))
#print(avg_fitness_arr)
#max_fitness_arr1 = max_fitness_arr[: : -1]
np_array1 = np.array(avg_fitness_arr)
np_array2 = np.array(max_fitness_arr)
x = np.arange(0, 10, 1)
#max_fitness_arr = max_fitness_arr.reverse(True)
#max_fitness_arr = reversed()
#plt.plot([i for i in range(1, 11, 1)], np_array2, label = "max_fitness")
plt.plot([i for i in range(1, 1 + ITERATIONS_SIZE, 1)], np_array2)
plt.show()
print("最大值:", max(np_array2))
实验结果
实验结果如下图所示:

总结
通过这次实验,我学会了如何运用遗传算法解决实际问题,并且对编码、以及相关术语,如:基因型、 表现型等有了一个更加深入的了解,收获颇丰。
